椭圆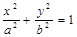
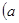 >
> >
>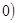 与直线
与直线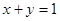 交于
交于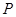 、
、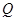 两点,且
两点,且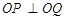 ,其中
,其中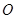 为坐标原点.
为坐标原点.
(1)求 的值;
的值;
(2)若椭圆的离心率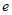 满足
满足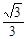 ≤
≤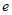 ≤
≤ ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.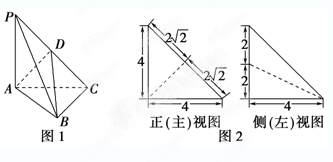
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
设直线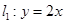 与直线
与直线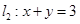 交于
交于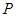 点.
点.
(1)当直线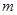 过
过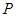 点,且与直线
点,且与直线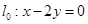 垂直时,求直线
垂直时,求直线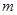 的方程;
的方程;
(2)当直线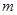 过
过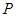 点,且坐标原点
点,且坐标原点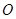 到直线
到直线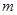 的距离为
的距离为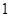 时,求直线
时,求直线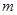 的方程.
的方程.
如果实数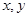 满足
满足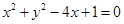 求:
求:
(1)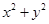 的最值;
的最值;
(2)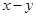 的最大值.
的最大值.
已知全集 ,集合
,集合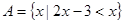 ,集合
,集合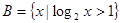 ;
;
(1)求集合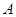 、
、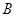 ; (2)求
; (2)求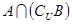 .
.
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.