(本小题满分12分)
已知数列 和
和 满足:
满足: ,
,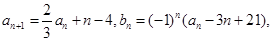 其中
其中 为实数,
为实数, 为正整数.
为正整数.
(1)对任意实数 ,证明数列
,证明数列 不是等比数列;
不是等比数列;
(2)试判断数列 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(3)设 ,
,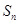 为数列
为数列 的前
的前 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
已知集合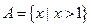 ,
,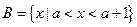 .
.
(1)若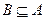 ,求实数
,求实数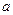 的取值范围;
的取值范围;
(2)若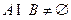 ,求实数
,求实数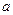 的取值范围.
的取值范围.
已知命题
 ,满足
,满足 ,命题
,命题

 ,方程
,方程 都表示焦点在
都表示焦点在 轴上的椭圆.若命题
轴上的椭圆.若命题 为真命题,
为真命题, 为假命题,求
为假命题,求 实数
实数 的取值范围
的取值范围
在圆
 上任取一点
上任取一点 ,过点
,过点 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足.当点
为垂足.当点 在圆上运动时,线段
在圆上运动时,线段 的中点
的中点 形成轨迹
形成轨迹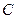 .
.
(1)求轨迹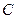 的方程;
的方程;
(2)若直线 与曲线
与曲线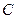 交于
交于 两点,
两点, 为曲线
为曲线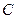 上一动点,求
上一动点,求 面积的最大值
面积的最大值
如图,设 点是圆
点是圆 上的动点,过点
上的动点,过点
 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为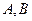 ,切线
,切线 分别交
分别交 轴于
轴于 两点.
两点.
(1)求四边形 面积的最小值;
面积的最小值;
(2)是否存在点 ,使得线段
,使得线段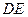 被圆
被圆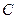 在点
在点 处的切线平分?若存在,求出点
处的切线平分?若存在,求出点 的纵坐标
的纵坐标 ;若不存在,说明理由.
;若不存在,说明理由.
如图,在平行四边形 中,
中, ,
, ,
, 为线段
为线段 的中线,将△
的中线,将△ 沿
沿 直线
直线 翻折成△
翻折成△ ,使平面
,使平面 ⊥平面
⊥平面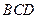 ,
,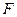 为线
为线 段
段 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)设 为线段
为线段 的中点,求直线
的中点,求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.