写出下列命题的“非P”命题,并判断其真假:
(1)若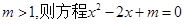 有实数根.
有实数根.
(2)平方和为0的两个实数都为0.
(3)若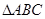 是锐角三角形, 则
是锐角三角形, 则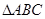 的任何一个内角是锐角.
的任何一个内角是锐角.
(4)若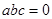 ,则
,则 中至少有一为0.
中至少有一为0.
(5)若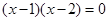 ,则
,则 .
.
(本小题满分14分)
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表: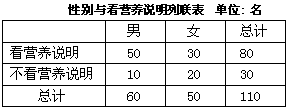
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为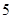 的样本,问样本中看与不看营养说明的女生各有多少名?
的样本,问样本中看与不看营养说明的女生各有多少名?
(2) 从(1)中的5名女生样本中随机选取两名作深度访谈, 求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
(本小题满分12分)
已知数列 是一个等差数列,且
是一个等差数列,且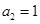 ,
,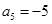 .(1)求
.(1)求 的通项
的通项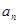 ;
;
(2) 求 前
前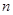 项和
项和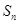 ;
;
在△ABC中,角A、B、C所对的边分别为a、b、c(其中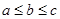 ),设向量
),设向量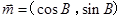 ,
,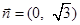 ,且向量
,且向量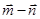 为单位向量.(模为1的向量称作单位向量)
为单位向量.(模为1的向量称作单位向量)
(1)求∠B的大小;
(2)若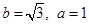 ,求△ABC的面积.
,求△ABC的面积.
一船由甲地逆水驶至乙地,甲、乙两地相距 S (km),水的流速为常量a(km/h),船在静水中的最大速度为b (km/h) (b>2a),已知船每小时的燃料费用(单位:元)与船在静水中的速度 v(km/h) 的平方成正比,比例系数为 k ,问:
(1)船在静水中的航行速度 v 为多少时,全程燃料费用最少?
(2)若水速 a =" 8.4" km/h,船在静水中的最大速度为b="25" km/h,要使全程燃料费用不超过40 k S元,求船在静水中的航行速度v 的范围。
已知等比数列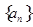 的前
的前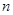 项和为
项和为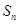 ,且
,且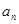 是
是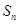 与2的等差中项,
与2的等差中项,
等差数列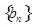 中,
中,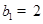 ,点
,点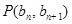 在直线
在直线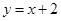 上.
上.
⑴求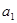 和
和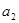 的值;
的值;
⑵求数列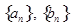 的通项
的通项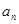 和
和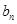 ;
;
⑶ 设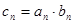 ,求数列
,求数列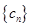 的前n项和
的前n项和 .
.