一船由甲地逆水驶至乙地，甲、乙两地相距 S （km）,水的流速为常量a（km/h）,船在静水中的最大速度为b (km/h) (b>2a)，已知船每小时的燃料费用(单位：元)与船在静水中的速度 v（km/h） 的平方成正比，比例系数为 k ,问：
（1）船在静水中的航行速度 v 为多少时，全程燃料费用最少？
（2）若水速 a =" 8.4" km/h，船在静水中的最大速度为b="25" km/h,要使全程燃料费用不超过40 k S元，求船在静水中的航行速度v 的范围。
设
、
是椭圆
上的两点，点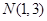
是线段
的中点，线段的垂直平分线与椭圆相交于
、
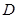两点．
（Ⅰ）求直线的方程；
（Ⅱ）求以线段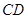
的中点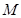
为圆心且与直线相切的圆的方程．
已知等差数列{an}的前三项为
，记前n项和为Sn
（Ⅰ）设
，求a和k的值；
（Ⅱ）设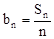
，求
的值
甲、乙两人各抛掷一次正方体骰子（它们的六个面分别标有数字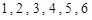
），设甲、乙所抛掷骰子朝上的面的点数分别为
、
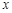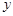，那么。
（I）共有多少种不同的结果？。
（II）请列出满足复数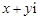
的实部大于虚部的所有结果。。
（III）满足复数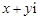的实部大于虚部的概率是多少？
正方体
，
，
为棱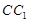
的中点，AC与BD交于点O．（1）求证：
（2）求证：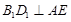
；
（3）求三棱锥
的体积．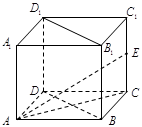
在△ABC中，a、b、c分别是角A、B、C的对边，且
，
（Ⅰ）求角B的大小；
（Ⅱ）若
最大边的边长为
，且
，求最小边长