已知椭圆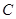 的中心在原点
的中心在原点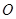 ,离心率
,离心率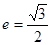 ,右焦点为
,右焦点为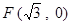 .
.
(Ⅰ)求椭圆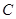 的方程;
的方程;
(Ⅱ)设椭圆的上顶点为 ,在椭圆
,在椭圆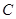 上是否存在点
上是否存在点 ,使得向量
,使得向量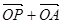 与
与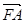 共线?若存在,求直线
共线?若存在,求直线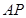 的方程;若不存在,简要说明理由.
的方程;若不存在,简要说明理由.
(本小题满分10分)已知两直线 和直线
和直线 ,试确定
,试确定 的值,使
的值,使
(1) 和
和 相交于点
相交于点 ;
;
(2) 且
且 在y轴上的截距为
在y轴上的截距为 .
.
已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn,且有Sn=2bn-1,
(1)求{an},{bn}的通项公式.
(2)若cn=anbn,{cn}的前n项和为Tn,求Tn.
在 中,
中, 的对边分别为
的对边分别为 ,已知
,已知
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求 的面积.
的面积.
(本题10分)已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD.
(1)求证:PF⊥FD;
(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.
(本题10分)已知直线l:x+2y-2=0,试求:
(1)点P(-2,-1)关于直线l的对称点坐标;
(2)直线l1:y=x-2关于直线l对称的直线l2的方程;
(3)直线l关于点(1,1)对称的直线方程.