（本小题满分12分）某市规定，高中学生三年在校期间参加不少于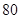
小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段
，
，
，
，
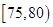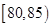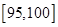（单位：小时）进行统计，其频率分布直方图如图所示．
（1）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（2）从全市高中学生（人数很多）中任意选取3位学生，记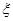
为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量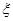的分布列和数学期望
.
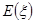(本小题满分12分）
甲乙两个学校高三年级分别有1100人，1000人，为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况，采用分层抽样方法从两个学校一共抽取了 105名学生的数学成绩，并作出了如下的频数分布统计表，规定考试成绩在[120，150]内为优秀，甲校：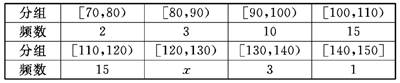
乙校：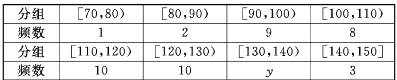
(I )计算x，y的值;
(II)由以上统计数据填写右面2X2列联表，若按是否优秀来判断，是否有97.5% 的把握认为两个学校的数学成绩有差异.
(III)根据抽样结果分别估计甲校和乙校的优秀率；若把频率作为概率，现从乙校学生中任取3人，求优秀学生人数
的分布列和数学期望;
附：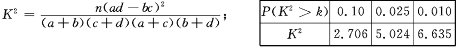
(本小题满分12分）
如图，已知四棱锥P—ABCD，侧面PAD为边长等于2的正三角形，底面ABCD为菱形，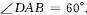
，
(I)证明：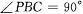
；
(II)若PB =3，求直线AB与平面PBC所成角的正弦值.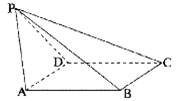
. (本小题满分12分）
已知函数
(I)求函数f(x)的单调递增区间；
(II)记ΔABC的内角A、B、C所对的边长分别为a,b,c，若
，ΔABC的面积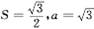
，求b +c的值.
．(本小题满分10分)选修4－5：不等式选讲
已知函数f(x)=|x－a|－2|x－1|（a∈R）.
(Ⅰ)当a=3时，求函数f(x)最大值；
(Ⅱ)解关于x的不等式f(x)≥0.
(本小题满分10分)选修4－1：几何证明选讲
如图，锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点.
(Ⅰ)求证：四点A，I，H，E共圆；
(Ⅱ)若∠C＝50°，求∠IEH的度数.