设函数 的最大值为M,最小正周期为T.
的最大值为M,最小正周期为T.
(Ⅰ)求M、T;
(Ⅱ)10个互不相等的正数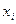 满足
满足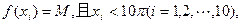 求
求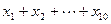 的值.
的值.
(理科)如图,已知⊙ :
: 及点
及点
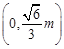 ,在⊙
,在⊙ 上任取一点
上任取一点 ′,连
′,连
 ′,并作
′,并作
 ′的中垂线l,设l与
′的中垂线l,设l与
 ′交于点P, 若点
′交于点P, 若点 ′取遍⊙
′取遍⊙ 上的点.
上的点.
(1)求点P的轨迹C的方程;
(2)设直线 与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若
与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若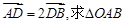 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
(文科)已知椭圆 的左、右两个顶点分别为A,B,直线
的左、右两个顶点分别为A,B,直线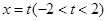 与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
(1)求证:无论t如何变化,圆C1与圆C2的圆心距是定值;
(2)当t变化时,求圆C1与圆C2的面积的和S的最小值.
(理科)已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4。
(Ⅰ)求椭圆的方程;
(Ⅱ)直线 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程。
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程。
(文科)
|
已知椭圆 :
: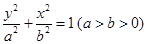 的右顶点为
的右顶点为 ,过
,过 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为 .
.

 的方程;
的方程;
 在抛物线
在抛物线 :
: 上,
上, 在点
在点 处的切线与
处的切线与 交于点
交于点 .当线段
.当线段 的中点与
的中点与 的中点的横坐标相等时,求
的中点的横坐标相等时,求 的最小值.
的最小值.
(理科)如图,直线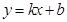 与椭圆
与椭圆 交于A、B两点,记
交于A、B两点,记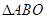 的面积为
的面积为 。
。
(Ⅰ)求在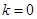 ,
,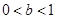 的条件下,
的条件下, 的最大值;
的最大值;
(Ⅱ)当 时,求直线AB的方程。
时,求直线AB的方程。