设F为抛物线E: 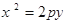
 的焦点,A、B、C为该抛物线上三点,已知
的焦点,A、B、C为该抛物线上三点,已知 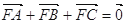 且
且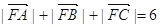 .
.
(1)求抛物线方程;
(2)设动直线l与抛物线E相切于点P,与直线 相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
已知函数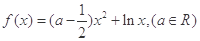 .
.
(Ⅰ)当 时,求
时,求 在区间
在区间 上的最大值;
上的最大值;
(Ⅱ)若在区间(1, +∞)上,函数 的图象恒在直线
的图象恒在直线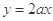 下方,求
下方,求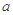 的取值范围.
的取值范围.
已知椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线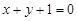 与以椭圆
与以椭圆 的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设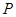 为椭圆
为椭圆 上一点,若过点
上一点,若过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点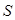 和
和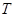 ,满足
,满足 (
( 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围.
已知某班学生语文与数学的学业水平测试成绩抽样统计如下表,若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示语文成绩与数学成绩.例如:表中语文成绩为B等级的共有20+18+4=42人.已知x与y均为B等级的概率是0.18.
(Ⅰ)求抽取的学生人数;
(Ⅱ)设该样本中,语文成绩优秀率是30%,求a,b值;
(Ⅲ)已知 求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率.
求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率.
如图,在直三棱柱 中,
中,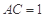 ,
,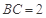 ,
,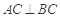 ,
, 分别为棱
分别为棱 的中点.
的中点.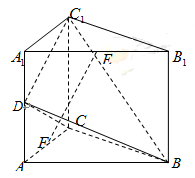
(Ⅰ)求证: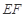 ∥平面
∥平面 ;
;
(Ⅱ)若异面直线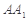 与
与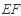 所成角为
所成角为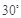 ,求三棱锥
,求三棱锥 的体积.
的体积.
设数列{an}满足:a1=1,an+1=3an,n∈N*.设Sn为数列{bn}的前n项和, 已知b1≠0,2bn–b1=S1 Sn,n∈N*.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bn log3 an,求数列{cn}的前n项和Tn .