某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过 小时收费
小时收费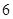 元,超过
元,超过 小时的部分每小时收费
小时的部分每小时收费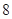 元(不足
元(不足 小时的部分按
小时的部分按 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过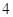 小时.
小时.
(1)若甲停车 小时以上且不超过
小时以上且不超过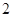 小时的概率为
小时的概率为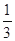 ,停车付费多于
,停车付费多于 元的概率为
元的概率为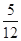 ,求甲停车付费恰为
,求甲停车付费恰为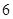 元的概率;
元的概率;
(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为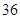 元的概率.
元的概率.
(本小题满分10分)选修4-5:不等式选讲
(Ⅰ)解不等式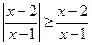 ;
;
(Ⅱ)设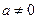 ,不等式
,不等式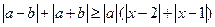 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在极坐标系中,已知圆 的圆心坐标为
的圆心坐标为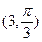 ,半径为
,半径为 ,点
,点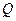 在圆周上运动,
在圆周上运动,
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)设直角坐标系的原点与极点 重合,
重合,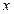 轴非负半轴与极轴重合,
轴非负半轴与极轴重合, 为
为 中点,求点
中点,求点 的参数方程.
的参数方程.
如图 中
中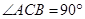 ,
, 是
是 的中点,
的中点, ,垂足为
,垂足为 .求证:
.求证: .
.
设函数 ,
,
(1)若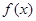 在
在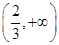 上存在单调增区间,求实数
上存在单调增区间,求实数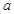 的取值范围;
的取值范围;
(2)当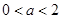 时
时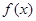 在
在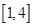 上的最小值为
上的最小值为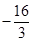 ,求
,求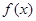 在该区间上的最大值.
在该区间上的最大值.
已知数列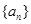 的前
的前 项和为
项和为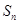 ,函数
,函数 (其中
(其中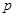 ,
,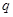 为常数且
为常数且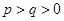 )
)
(1)若当 时,函数
时,函数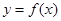 取得极大值,求
取得极大值,求 的值;
的值;
(2)若当 时,函数
时,函数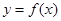 取得极小值,点
取得极小值,点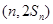 ,
,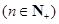 都在函数
都在函数 的图像上,(
的图像上,(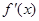 是
是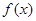 的导函数),求数列
的导函数),求数列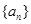 的通项公式.
的通项公式.