已知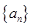 是等差数列,
是等差数列,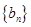 是各项为正数的等比数列,且
是各项为正数的等比数列,且 ,
,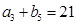 ,
,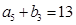 .
.
(Ⅰ)求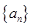 和
和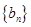 通项公式;
通项公式;
(Ⅱ)若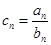 ,求数列
,求数列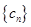 的前
的前 项和
项和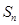 .
.
已知椭圆C: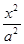 +
+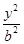 =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+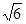 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同 两点A,B且线段AB的垂直平分线过定点C(
两点A,B且线段AB的垂直平分线过定点C(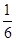 ,0)求实数k的取值范围。
,0)求实数k的取值范围。
如图, 在梯形
在梯形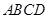 中,
中,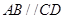 ,
,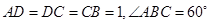 ,四边
,四边
形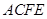
 为矩形,平面
为矩形,平面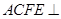 平面
平面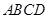 ,
,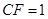 .
.
(I)求证: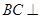 平面
平面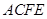 ;
;
(II)点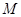 在线段
在线段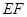 上运动,设
上运动,设 平面
平面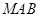 与平面
与平面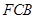 所成二面角的平面角为
所成二面角的平面角为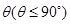 ,试求
,试求 的取值范围.
的取值范围.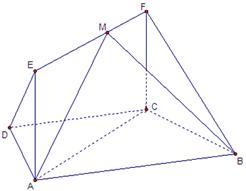
已知数列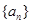 满足:
满足: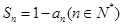 ,其中
,其中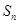 为数列
为数列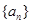 的前
的前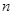 项和.
项和.
(1)试求数列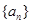 的通项公式;
的通项公式;
(2)设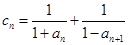 ,数列
,数列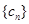 的前
的前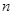 项和为
项和为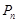 ,求证
,求证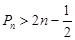
△ABC的三个角A,B,C所对的边分别是a,b,c,向量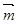 =(2,-1),
=(2,-1),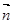 =(sinBsinC,
=(sinBsinC,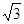 +2cosBcosC),且
+2cosBcosC),且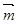 ⊥
⊥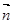 。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(
。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(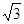 +1)sinB=0;③a=2。试从中再选择两个条件以确定△ABC,并求出所确定的△
+1)sinB=0;③a=2。试从中再选择两个条件以确定△ABC,并求出所确定的△ ABC的面积。
ABC的面积。
.将编号为1,2,3的三个小球随意放入编号为1,2,3的三个纸箱中,每个纸箱内有且只有一个小球,称此为一轮“放球”,设一轮“放球”后编号为i(i=1,2,3)的纸箱放入的小球编号为ai,定义吻合度误差为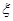 =|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足
=|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足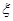 =2时的概率。⑵
=2时的概率。⑵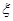 的数学期望。
的数学期望。