我们知道:圆的任意一弦(非直径)的中点和圆心的连线与该弦垂直;那么,若椭圆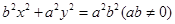 的一弦(非过原点的弦)中点与原点的连线及弦所在直线的斜率均存在,你能得到什么结论?请予以证明.
的一弦(非过原点的弦)中点与原点的连线及弦所在直线的斜率均存在,你能得到什么结论?请予以证明.
(本小题满分12分)如图,四边形 是边长为
是边长为 的正方形,
的正方形, 、
、 分别是边
分别是边 、
、 上的点(M不与A、D重合),且
上的点(M不与A、D重合),且 ,
, 交
交 于点
于点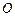 ,沿
,沿 将正方形折成直二面角
将正方形折成直二面角
(1)当 平行移动时,
平行移动时,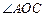 的大小是否发生变化?试说明理由;
的大小是否发生变化?试说明理由;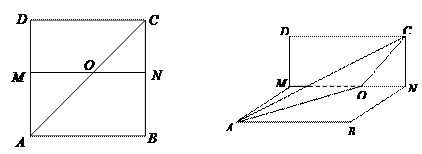 (2)当
(2)当 在怎样的位置时,
在怎样的位置时, 、
、 两点间的距离最小?并求出这个最小值.
两点间的距离最小?并求出这个最小值.
(本小题满分12分)已知 展开式的二项式系数之和比
展开式的二项式系数之和比 展开式的二项式系数之和小
展开式的二项式系数之和小 .
.
(1)求 ;
;
(2)求 的第二项的系数和
的第二项的系数和 的第
的第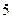 项.
项.
(本小题满分14分)设函数 (a、b、c、d∈R)图象关于原点对称,且x=1时,
(a、b、c、d∈R)图象关于原点对称,且x=1时, 取极小值
取极小值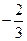 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若对任意的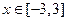 ,恒有
,恒有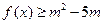 成立,求
成立,求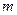 的取值范围;
的取值范围;
(Ⅲ)当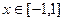 时,函数
时,函数 图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
(IV)设 表示的曲线为G,过点
表示的曲线为G,过点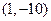 作曲线G的切线
作曲线G的切线 ,求
,求 的方程.
的方程.
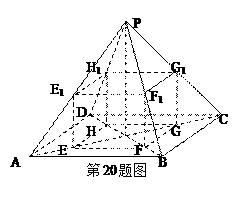
(本小题满分13分)已知正四棱锥P—ABCD的高为 ,底面边长为
,底面边长为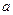 ,其内接正四棱柱EFGH—E1F1G1H1的四个顶点E、F、G、H在底面上,另外四个顶点E1、F1、G1、H1分别在棱PA、PB、PC、PD上(如图所示),设正四棱柱的底面边长为
,其内接正四棱柱EFGH—E1F1G1H1的四个顶点E、F、G、H在底面上,另外四个顶点E1、F1、G1、H1分别在棱PA、PB、PC、PD上(如图所示),设正四棱柱的底面边长为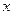 .
.
(Ⅰ)设内接正四棱柱的体积为 ,求出函数
,求出函数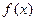 的解析式;
的解析式;
(Ⅱ)试求该内接正四棱柱的最大体积及对应的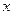 的值.
的值.
(本小题满分12分)由0,2,5,6,7,8这六个数字组成没有重复数字的四位自然数(解答给出简单的理由).
(Ⅰ)共能得到多少个这样的四位数?
(Ⅱ)设这样得到的四位奇数有 个,四位偶数有
个,四位偶数有 个,求
个,求 的值;
的值;
(Ⅲ)将所得到的所有四位数从小到大排成数列 ,求
,求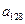 .
.