已知函数 .
.
(1)作出函数 的图象;
的图象;
(2)写出函数 的单调区间;
的单调区间;
(3)判断函数 的奇偶性,并用定义证明.
的奇偶性,并用定义证明.
(本小题满分12分)
已知数列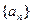 为等差数列,其前
为等差数列,其前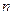 项和为
项和为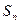 ,且
,且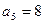 ,
,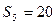
(1) 求
求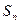 ;
;
(2)若对任意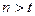 ,
, ,都有
,都有
求 的最小值。
的最小值。
(本小题满分 12分)
12分)
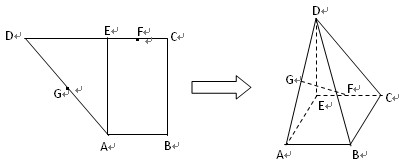
已知直角梯形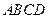 中,
中,

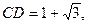 过
过 作
作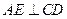 ,垂足为
,垂足为 ,
,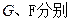
 的中点,现将
的中点,现将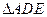 沿
沿 折叠,使得
折叠,使得 ,
,
(1)求证: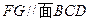 ;
;
(2)设四棱锥D-ABCE的体积为 V,其外接球体积为
V,其外接球体积为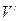 ,求V
,求V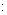
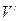 的值.
的值.
(本小题满分12分)
已知集合
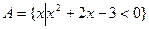 ,
, .
.
(1)在区间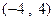 上任取一个实数
上任取一个实数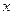 ,求“
,求“ ”的概率;
”的概率;
(2)设 为有序实数对,其中
为有序实数对,其中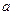 是从集合
是从集合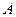 中任取的一个整数,
中任取的一个整数,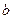 是从集合
是从集合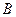 中任取的一个整
中任取的一个整 数,求“
数,求“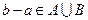 ”的概率.
”的概率.
(本小题满分12分)
在 中,内角
中,内角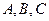 所对边长分别为
所对边长分别为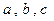 ,
, ,
,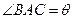 ,
, .
.
(1)求 的最大值及
的最大值及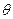 的取值范围;
的取值范围;
(2)求 函数
函数 的最值.
的最值.
(本小题满分14分)
现有甲,乙,丙,丁四名篮球运动员进行传球训练,由甲开始传球(即第一次传球是由甲传向乙或丙或丁),记第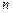 次传球球传回到甲的不同传球方式种数为
次传球球传回到甲的不同传球方式种数为 .
.
(1)试写出 ,
, 并找出
并找出
 与
与 (
( )的关系式;
)的关系式;
(2)求数列 的通项公式;
的通项公式;
(3)证明:当 时,
时, 
 .
.