(本小题满分10分)已知中心在原点O,焦点在 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为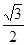 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为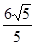 。
。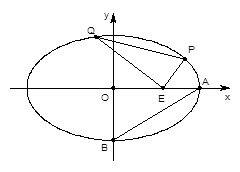
(1)求椭圆C的标准方程;
(2)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足EP⊥EQ,
求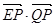 的取值范围.
的取值范围.
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格(将答案直接填在表格内),并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
(12分) 如图,在四边形 中,
中,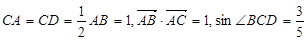 .
.
(1)求边 的长;
的长;
(2)求四边形 的面积;
的面积;
(3)求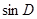 的值.
的值. 
已知椭圆的参数方程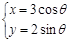 (
(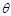 为参数),求椭圆上一点P到直线
为参数),求椭圆上一点P到直线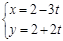 (
(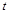 为参数)的最短距离。
为参数)的最短距离。
如图,在⊙O中,弦CD垂直于直径AB,
求证: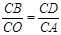 。
。
设函数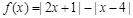
(1)解不等式 ;
;
(2)若关于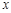 的不等式
的不等式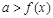 有解,求实数
有解,求实数 的取值范围。
的取值范围。