选择你所熟悉的实物模型作出它的俯视图、主视图及左视图.
端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转装盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得元购物券,最多可得元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.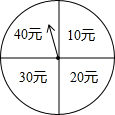
已知关于x、y的方程组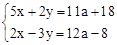 的解满足x>0,y>0,求实数a的取值范围.
的解满足x>0,y>0,求实数a的取值范围.
(1)计算: ;
;
(2)先化简,再求值: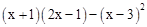 ,其中x=-2.
,其中x=-2.
在 ABCD中,P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连结CE,CP.已知∠A=60°;
ABCD中,P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连结CE,CP.已知∠A=60°;
(1)若BC=8,AB=6,当AP的长为多少时,△CPE的面积最大,并求出面积的最大值.
(2)试探究当△CPE≌△CPB时, ABCD的两边AB与BC应满足什么关系?
ABCD的两边AB与BC应满足什么关系?
如图1,在一直角边长为4米的等腰直角三角形地块的每一个正方形网格的格点(纵横直线的交点及三角形顶点) 上都种植同种农作物,根据以往种植实验发现,每株农作物的产量y(单位:千克) 受到与它周围直线距离不超过1米的同种农作物的株数x(单位:株) 的影响情况统计如下表:
| x(株) |
1 |
2 |
3 |
4 |
| y(千克) |
21 |
18 |
15 |
12 |
(1)通过观察上表,猜测y与x之间之间存在哪种函数关系,求出函数关系式并加以验证;
(2)根据种植示意图填写下表,并求出这块地平均每平方米的产量为多少千克?
| y(千克) |
21 |
18 |
15 |
12 |
| 频数 |
(3)有人为提高总产量,将上述地块拓展为斜边长为6米的等腰直角三角形,采用如图2所示的方式,在每个正方形网格的格点上都种植了与前面相同的农作物,共种植了16株,请你通过计算平均每平方米的产量,来比较那种种植方式更合理?