(本小题满分16分)如图, 是椭圆
是椭圆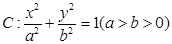 的左、右顶点,椭圆
的左、右顶点,椭圆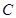 的离心率为
的离心率为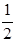 ,右准线
,右准线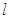 的方程为
的方程为 .
.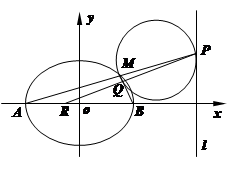
(1)求椭圆方程;
(2)设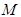 是椭圆
是椭圆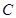 上异于
上异于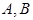 的一点,直线
的一点,直线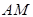 交
交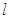 于点
于点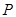 ,以
,以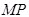 为直径的圆记为
为直径的圆记为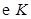 .
.
①若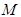 恰好是椭圆
恰好是椭圆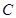 的上顶点,求
的上顶点,求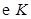 截直线
截直线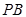 所得的弦长;
所得的弦长;
②设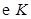 与直线
与直线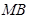 交于点
交于点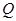 ,试证明:直线
,试证明:直线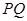 与
与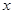 轴的交点
轴的交点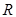 为定点,并求该定点的坐标.
为定点,并求该定点的坐标.
(本小题满分12分)
在△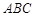 中,已知
中,已知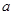 、
、 、
、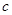 分别是三内角
分别是三内角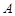 、
、 、
、 所对应的边长,且
所对应的边长,且
(Ⅰ)求角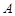 的大小;
的大小;
(Ⅱ)若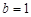 ,且△
,且△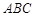 的面积为
的面积为 ,求
,求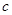 .
.
(本小题满分12分)
已知数列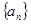 的前
的前 项和为
项和为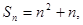
(1)求数列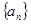 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列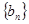 的前
的前 项和
项和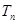 .
.
(本小题满分8分)
已知数列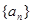 的通项公式
的通项公式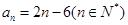 .
.
(1)求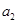 ,
, ;
;
(2)若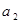 ,
, 分别是等比数列
分别是等比数列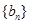 的第1项和第2项,求数列
的第1项和第2项,求数列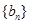 的通项公式
的通项公式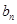 .
.
设数列{ n}满足
n}满足 1=
1= ,
, n+1=
n+1= n2+
n2+ 1,
1,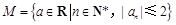 .
.
(Ⅰ)当 ∈(-∞,-2)时,求证:
∈(-∞,-2)时,求证: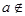 M;
M;
(Ⅱ)当 ∈(0,
∈(0,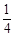 ]时,求证:
]时,求证: ∈M;
∈M;
(Ⅲ)当 ∈(
∈(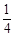 ,+∞)时,判断元素
,+∞)时,判断元素 与集合M的关系,并证明你的结论.
与集合M的关系,并证明你的结论.
某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立. 又知电梯只在有人下时才停止.
(Ⅰ)求某乘客在第 层下电梯的概率
层下电梯的概率 ;
;
(Ⅱ)求电梯在第2层停下的概率;
(Ⅲ)求电梯停下的次数 的数学期望.
的数学期望.