(本小题满分12分)如图,三棱柱 的各棱长均为2,侧面
的各棱长均为2,侧面
 底面
底面 ,侧棱
,侧棱 与底面
与底面 所成的角为
所成的角为 .
.
(1) 求直线 与底面
与底面 所成的角;
所成的角;
(2) 在线段 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分).
设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.
某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.
(1)根据以上数据建立一个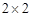 的列联表;
的列联表;
(2)认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考数值: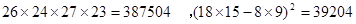 )
)
已知复数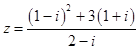 ,若
,若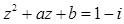 ,
,
(1)求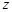 ;
;
(2)求实数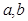 的值.
的值.
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
| 年份200x(年) |
0 |
1 |
2 |
3 |
4 |
| 人口数y(十万) |
5 |
7 |
8 |
11 |
19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求最小二乘法求出y关于x的线性回归方程y=bx+a;
(3) 据此估计2012年.该 城市人口总数.
(参考数值:0×5+1×7+2×8+3×11+4×19=132, ,公式见卷首)
,公式见卷首)
(本小题满分14分)
已知函数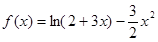 .
.
(1)求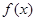 在[0,1]上的极值;
在[0,1]上的极值;
(2)若对任意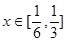 ,不等式
,不等式 成立,求实数
成立,求实数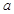 的取值范围;
的取值范围;
(3)若关于 的方程
的方程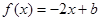 在[0,1]上恰有两个不同的实根,求实数
在[0,1]上恰有两个不同的实根,求实数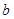 的取值范围.
的取值范围.