某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
| 年份200x（年） |
0 |
1 |
2 |
3 |
4 |
| 人口数y（十万） |
5 |
7 |
8 |
11 |
19 |
(1)请画出上表数据的散点图；
(2)请根据上表提供的数据，求最小二乘法求出y关于x的线性回归方程y=bx+a；
(3) 据此估计2012年.该 城市人口总数.
(参考数值：0×5+1×7+2×8+3×11+4×19=132，
，公式见卷首)
（本小题满分12分）已知双曲线C: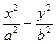
=1（a＞0，b＞0）的一条准线方程为x=
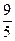，一个顶点到一条渐近线的距离为
.
（1）求双曲线C的方程；
（2）动点P到双曲线C的左顶点A和右焦点F的距离之和为常数（大于|AF|），且cosAPF的最小值为－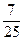
，求动点P的轨迹方程.
（本小题满分12分）某厂生产一种仪器，由于受生产能力和技术水平的限制，会产生一些次品，根据经验知该厂生产这种仪器，次品率p与日产量x（件）之间大体满足关系：
.已知每生产一件合格的仪器可盈利A元，但每生产一件次品将亏损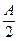
元，厂方希望定出适当的日产量.
（1）试判断：当日产量（件）超过94件时，生产这种仪器能否赢利？并说明理由；
（2）当日产量x件不超过94件时，试将生产这种仪器每天的赢利额T（元）表示成日产量x（件）的函数；
（3）为了获得最大利润，日产量x件应为多少件？
（本小题满分12分）在△OAB中，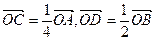
，AD与BC交于点M，设
=a，
=b，
（1）用a，b表示
;
（2）在线段AC上取一点E，在线段BD上取一点F，使EF过M点，设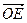
=p，
=q，求证：
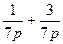=1.
（本小题满分12分）如图，已知：PD⊥平面ABCD，AD⊥DC，AD∥BC，PD∶DC∶BC=1∶1∶
.
（1）求PB与平面PDC所成角的大小；
（2）求二面角D—PB—C的正切值.
（本小题满分12分）已知等差数列｛an｝的首项a1=1，公差d>0，且其第二项、第五项、第十四项分别是等比数列｛bn｝的第二、三、四项.
（1）求数列｛an｝与｛bn｝的通项公式；
（2）设数列｛cn｝对任意自然数n均有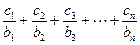
=an+1成立，求c1+c2+c3+…+c2003的值.