水以20米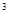 /分的速度流入一圆锥形容器,设容器深30米,上底直径12米,试求当水深10米时,水面上升的速度.
/分的速度流入一圆锥形容器,设容器深30米,上底直径12米,试求当水深10米时,水面上升的速度.
(本小题满分14分)如图,已知椭圆 的离心率为
的离心率为  ,F1、F2为其左、右焦点,过F1的直线
,F1、F2为其左、右焦点,过F1的直线 交椭圆于A、B两点,△F1AF2的周长为
交椭圆于A、B两点,△F1AF2的周长为 .
.
(1)求椭圆的标准方程;
(2)求△AOB面积的最大值(O为坐标原点);
(3)直线m也过F1与且与椭圆交于C、D两点,且 ,设线段AB、CD的中点分别为M、N两点,试问:直线MN是否过定点?若是,求出定点坐标;若不是,请说明理由.
,设线段AB、CD的中点分别为M、N两点,试问:直线MN是否过定点?若是,求出定点坐标;若不是,请说明理由.
(本小题满分13分)在平面直角坐标系中,已知点 ,点B在直线
,点B在直线 :
: 上运动,过点B与
上运动,过点B与 垂直的直线和线段AB的垂直平分线相交于点M.
垂直的直线和线段AB的垂直平分线相交于点M.
(1)求动点M的轨迹E的方程;
(2)过(1)中轨迹E上的点P (1,2)作两条直线分别与轨迹E相交于 ,
, 两点.试探究:当直线PC,PD的斜率存在且倾斜角互补时,直线CD的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
两点.试探究:当直线PC,PD的斜率存在且倾斜角互补时,直线CD的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
(本小题满分12分)已知等差数列 的首项
的首项 ,前n项和为Sn,且
,前n项和为Sn,且 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列{bn}为递增的等比数列,且集合 ,设数列
,设数列 的前n项和为
的前n项和为 ,求
,求 .
.
(本小题满分12分)设数列 的首项为1,前n项和为Sn,且
的首项为1,前n项和为Sn,且 (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, 是数列
是数列 的前n项和,求
的前n项和,求 .
.
(本小题满分12分)在直三棱柱 中,
中, ,
, , 异面直线
, 异面直线 与
与 所成的角等于
所成的角等于 ,设
,设 .
.
(1)求a的值;
(2)求平面 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.