设函数f(x)=ax3+bx2+cx+d的图象与y轴的交点为P,且曲线f(x)在P点出处的切线方程为24x+y-12=0,又函数在x=2出处取得极值-16,求该函数的单调递减区间.
(本小题满分12分)从广东省某市高三第一次模拟考试成绩中,随机抽取了 名学生的数学成绩得到频率分布直方图如图所示.
名学生的数学成绩得到频率分布直方图如图所示.
(Ⅰ)根据频率分布直方图,估计该市高三学生本次模拟考试数学成绩的平均分;
(Ⅱ)若用分层抽样的方法从分数在 和
和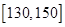 的学生中共抽取
的学生中共抽取 人,在这抽取的
人,在这抽取的 人中,随机抽取
人中,随机抽取 人,求分数在
人,求分数在 和
和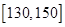 各
各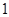 人的概率.
人的概率.
(本小题满分14分)已知函数 .
.
(1)求函数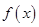 的单调区间;
的单调区间;
(2)设函数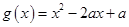 ,若对于任意
,若对于任意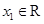 ,总存在
,总存在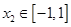 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆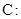
 (
(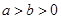 )的离心率为
)的离心率为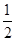 ,点
,点 在椭圆
在椭圆 上,
上,
过椭圆 的右焦点的动直线
的右焦点的动直线 与椭圆
与椭圆 相交于
相交于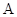 、
、 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若线段 中点的横坐标为
中点的横坐标为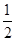 ,求直线
,求直线 的方程;
的方程;
(3)若线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点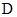 .设弦
.设弦 的中点为
的中点为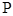 ,试求
,试求 的取值范围.
的取值范围.
(本小题满分14分)已知数列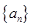 的前
的前 项和为
项和为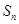 ,且点
,且点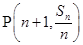 (
(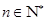 )均在函数
)均在函数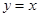 的图象上.
的图象上.
(1)求数列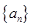 的通项公式;
的通项公式;
(2)设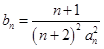 ,数列
,数列 的前
的前 项和为
项和为 ,证明:对于任意的
,证明:对于任意的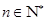 ,都有
,都有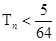 .
.
(本小题满分14分)如图,将一副三角板拼接,使他们有公共边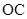 ,且使平面
,且使平面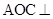 平面
平面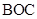 ,
,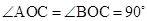 ,
,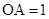 ,
, ,
,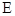 是
是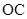 的中点.
的中点.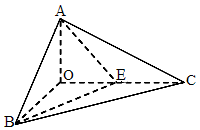
(1)求 点到平面
点到平面 的距离;
的距离;
(2)求二面角 的正弦值.
的正弦值.