某单位为了丰富职工的业余文化生活，决定在广场放映露天电影，小明和小强吃过晚饭手拉手来到广场，准备看电影，可小明非要在背面看，于是小强在正面，小明在背面，如图，如果他俩眼睛在同一水平面上，而且看同一点时视线与水平线夹角相等.利用三角形全等，能判断他俩距屏幕一样远吗？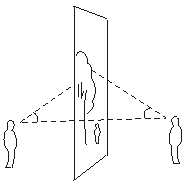
思考：结果为：___________.
证明：如图：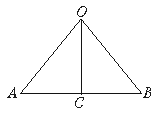
∠OAC=∠OBC
∵OC⊥AB
∴∠ACO=______=90°
在△OAC和△OBC中：
∠OAC=∠OBC
∠ACO=______
OC=______
∴△OAC≌△OBC，理由( ）.
因此判断他们距屏幕的距离_________.
如图，
ABCD中，G是CD上一点,BG交AD延长线于E，且AF=CG，∠DGE=980.
（1）求证:DF=BG；（2）试求∠AFD的度数．
解方程：（1）x2＋5x＋2＝0（2）（x－5）（3x－2）="10"
如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，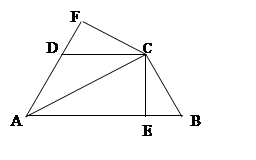
（1）试说明
.
（2）
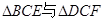全等吗？ 试说明理由.
（3）若AC=10，CE=6， AD=5,求DF的长
（4）若AB=21，AD=9，BC=CD=10，求AC的长。
如图，滑杆在机械槽内运动，∠ACB为直角，已知滑杆AB 长2.5米，顶端A在AC 上运动，量得滑杆下端B距C点的距离为1.5米，当端点B向右移动0.5米时，求滑杆顶端A下滑多少米？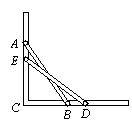
如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。