溶液自深度18 cm、顶部直径12 cm的圆锥形漏斗中，漏入一直径为10 cm的圆柱形筒中．开始时漏斗中盛满了水.已知当溶液在漏斗中的深度为12 cm时，其水面下落的速度为1 cm／min，问：此时圆柱彤筒中，水面上升的速度为多少?
如图，
均是边长为2的等边三角形，且它们所在平面互相垂直，
，
.
（1）求证：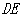 
|| 
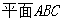
（2）求二面角
的余弦值。. 
（文）我国是世界上严重缺水的国家之一，城市缺水问题较为突出。某市政府为了节约生活用水，计划在本市试行居民生活用水定额管理，即确定一个居民月用水量的标准。为了确定一个较为合理的标准，必须先了解全市居民日常用水量的分布情况。现采用抽样调查的方式，获得了n位居民某年的月均用水量（单位：t），样本统计结果如下图表：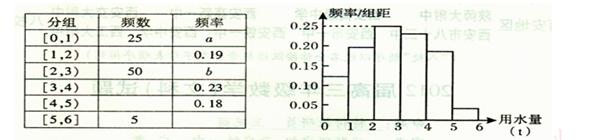
（1）分别求出n，a，b的值；
（2）若从样本中月均用水量在[5，6]（单位：t）的5位居民中任选2人作进一步的调查研究，求月均用水量最多的居民被选中的频率（5位居民的月均用水量均不相等。）
（理）已知甲盒内有大小相同的3个红球和4个黑球，乙盒内有大小相同的5个红球和4个黑球．现从甲、乙两个盒内各任取2个球．
（1）求取出的4个球均为红球的概率；
（2）求取出的4个球中恰有1个红球的概率；
设函数f (x)=2cosx (cosx+
sinx)－1, x∈R．
（1）求f (x)的最小正周期T及单调递增区间；
（2）在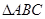
中，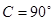
，求f (A)的取值范围．
已知函数
，
（1）求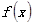
的单调区间和极值。 （2）求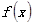在
上的最大值和最小值。