已知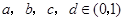 ,试比较
,试比较 与
与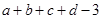 的大小.
的大小.
杨辉是中国南宋末年的一位杰出的数学家、数学教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第3个数;
(2)若第 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为 ,求
,求 的值;
的值;
(3)写出第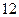 行所有数的和,写出
行所有数的和,写出 阶(包括
阶(包括 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35,我们发现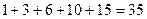 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第 斜列中(从右上到左下)前
斜列中(从右上到左下)前 个数之和,一定等于第
个数之和,一定等于第 斜列中第
斜列中第 个数.
个数.
试用含有 ,
,
 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.
甲、乙两人在罚球线投球命中的概率分别为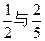 ,且各次投球相互之间没有影响.
,且各次投球相互之间没有影响.
(1)甲、乙两人在罚球线各投球一次,求这二次投球中恰好命中一次的概率;
(2)甲、乙两人在罚球线各投球二次,求这四次投球中至少有一次命中的概率.
已知直线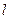 的参数方程为
的参数方程为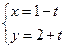 ,曲线
,曲线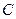 的极坐标方程为
的极坐标方程为 .
.
(1)将直线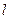 的参数方程化为普通方程;以极点为直角坐标系的原点,极轴为
的参数方程化为普通方程;以极点为直角坐标系的原点,极轴为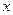 轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线
轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线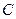 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若 为直线
为直线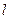 上任一点,
上任一点,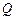 是曲线
是曲线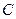 上任一点,求
上任一点,求 的最小值.
的最小值.
已知复数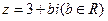 ,且
,且 为纯虚数.
为纯虚数.
(1)求复数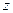 ;
;
(2)若 ,求复数
,求复数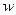 的模
的模 .
.
(本题满分14分) 设函数 .
.
(Ⅰ)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(Ⅱ)若函数 仅在x=0处有极值,试求a的取值范围;
仅在x=0处有极值,试求a的取值范围;
(Ⅲ)若对于任何 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.