设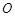 为坐标原点,已知向量
为坐标原点,已知向量 ,
, 分别对应复数
分别对应复数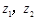 ,且
,且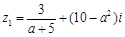 ,
, ,
, .若
.若 可以与任意实数比较大小,求
可以与任意实数比较大小,求 ,
, 的值.
的值.
如图,已知菱形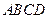 的边长为
的边长为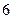 ,
,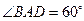 ,
,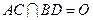 .将菱形
.将菱形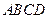 沿对角线
沿对角线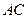 折起,使
折起,使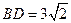 ,得到三棱锥
,得到三棱锥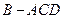 .
.
(Ⅰ)若点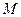 是棱
是棱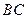 的中点,求证:
的中点,求证: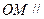 平面
平面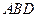 ;
;
(Ⅱ)求二面角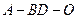 的余弦值;
的余弦值;
(Ⅲ)设点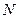 是线段
是线段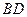 上一个动点,试确定
上一个动点,试确定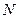 点的位置,使得
点的位置,使得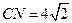 ,并证明你的结论
,并证明你的结论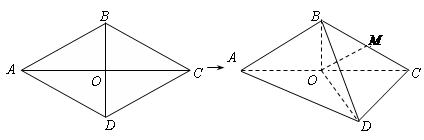
已知函数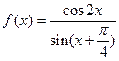 .
.
(Ⅰ)求函数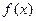 的定义域;
的定义域;
(Ⅱ)若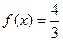 ,求
,求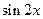 的值
的值
定义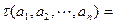
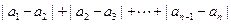 为有限项数列
为有限项数列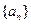 的波动强度.
的波动强度.
(Ⅰ)当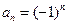 时,求
时,求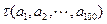 ;
;
(Ⅱ)若数列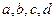 满足
满足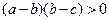 ,求证:
,求证: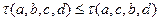 ;
;
(Ⅲ)设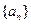 各项均不相等,且交换数列
各项均不相等,且交换数列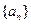 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列
中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列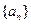 一定是递增数列或递减数列
一定是递增数列或递减数列
已知抛物线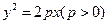 的焦点为
的焦点为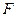 ,过
,过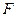 的直线交
的直线交 轴正半轴于点
轴正半轴于点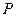 ,交抛物线于
,交抛物线于 两点,其中点
两点,其中点 在第一象限.
在第一象限.
(Ⅰ)求证:以线段 为直径的圆与
为直径的圆与 轴相切;
轴相切;
(Ⅱ)若 ,
,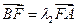 ,
, ,求
,求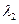 的取值范围.
的取值范围.
已知函数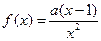 ,其中
,其中 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若直线 是曲线
是曲线 的切线,求实数
的切线,求实数 的值;
的值;
(Ⅲ)设 ,求
,求 在区间
在区间 上的最大值.
上的最大值.
(其中 为自然对数的底数)
为自然对数的底数)