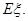已知命题p:方程x2+mx+1=0有两个不等的负根;命题q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
在等差数列{an}中,a1=-60,a17=-12.
(1)求通项公式an,(2)求此数列前30项的绝对值的和 。
(本小题满分14分)已知数列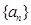 的前n项和
的前n项和 满足
满足 ,其中b是与n无关的常数,且
,其中b是与n无关的常数,且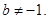
(1)求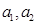 ;
;
(2)求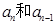 的关系式;
的关系式;
(3)猜想用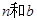 表示
表示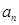 的表达式(须化简),并证明之。
的表达式(须化简),并证明之。
(本小题满分13分)已知m为实常数,设命题p:函数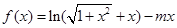 在其定义域内为减函数;命题
在其定义域内为减函数;命题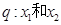 是方程
是方程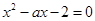 的两上实根,不等式
的两上实根,不等式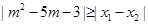 对任意实数
对任意实数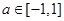 恒成立。
恒成立。
(1)当p是真命题,求m的取值范围;
(2)当“p或q”为真命题,“p且q”为假命题时,求m的取值范围。
(本小题满分12分)已知斜率为1的直线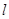 与双曲线
与双曲线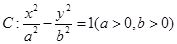 相交于B、D两点,且BD的中点为M(1,3)。
相交于B、D两点,且BD的中点为M(1,3)。
(1)求双曲线C的离心率;
(2)若双曲线C的右焦点坐标为(3,0),则以双曲线的焦点为焦点,过直线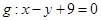 上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。
上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。
(本小题满分12分)某旅行社组织了一个有36名游客的旅游团到安徽风景名胜地旅游,其中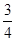 是省外游客,其余是省内游客,在省外游客中有
是省外游客,其余是省内游客,在省外游客中有 玩过黄山,在省内游客中有
玩过黄山,在省内游客中有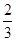 玩过黄山。
玩过黄山。
(1)在该团中随机采访3名游客,求恰有1名 省外游客玩过黄山且省内游客玩过黄山少于2人的概率;
(2)在该团的省内游客中随机采访3名游客,设其中省内游客玩过黄山的人数为随机变量 ,求
,求 的分布列及数学期望
的分布列及数学期望