某工厂有甲、乙两条生产线先后投产.在乙生产线投产以前,甲生产线已生产了200吨成品;从乙生产线投产开始,甲、乙两条生产线每天分别生产20吨和30吨成品.
(1)分别求出甲、乙两条生产线投产后,总产量y(吨)与从乙开始投产以来所用时间x(天)之间的函数关系式,并求出第几天结束时,甲、乙两条生产线的总产量相同;
(2)在如图所示的直角坐标系中,作出上述两个函数在第一象限内的图象;观察图象,分别指出第15天和第25天结束时,哪条生产线的总产量高?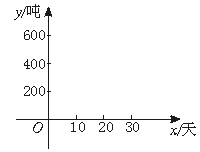
如图,△ABC是格点三角形,且A(-3,-2),B(-2,-3),C(1,-1).
(1)请在图中画出△ABC关于y轴的对称△A’B’C’.
(2)写出△A’B’C’各点坐标,并计算△A’B’C’的面积.
计算: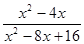 .
.
先化简,再求值:  ,其中x = -2,y =
,其中x = -2,y =  .
.
分解下列因式:
(1) .(2)
.(2)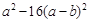 .
.
问题1:如图1,在四边形ABCD中,AD∥BC,∠A=∠D,AB=BC=CD,点M,N分别在AD,CD上,若∠MBN=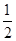 ∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;
∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;
问题2:如图2,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD的延长线上,若∠MBN=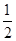 ∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.
∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明. 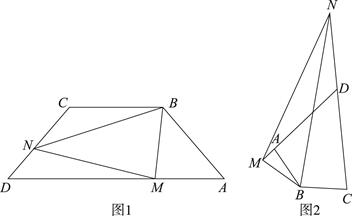
解:(1)猜想:____________________
(2)猜想:____________________
证明: