交5元钱,可以参加一次摸奖,一袋中有同样大小的球10个,其中8个标有1元钱,2个标有5元钱,摸奖者只能从中任取2个球,他所得奖励是所抽2球的钱数之和,求抽奖人所得钱数的分布列.
(本小题满分14分)为研究我校高二年级的男生身高,随机抽取40名男生,实测身高数据(单位:厘米)如下:
171 173 163 169 166 167 168.5 160 170 165
175 169 167 156 165.5 168 170 184 168 174
165 170 174 161 177 175.5 173 164 175 171.5
176 159 172 181 175.5 165 163 173 170.5 171
(I)依据题目提示作出频率分布表;
(Ⅱ)在(I)的条件下画出频率分布直方图并且画出其频率分布折线图;
(Ⅲ)试利用频率分布的直方图估计样本的平均数。
【解】(I)最低身高156cm,最高身高184cm,确定组距为4,作频率分布表如下:
| 身高(cm) |
频数累计 |
频数 |
频率(%) |
 |
|||
 |
(Ⅱ)频率直方图如下:
(本小题满分12分)圆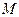 的圆心在直线
的圆心在直线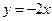 上,经过点
上,经过点 ,且与直线
,且与直线 相切,
相切,
(I)试求圆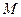 的方程;
的方程;
(Ⅱ)从点 发出的光线经直线
发出的光线经直线 反射后可以照在圆
反射后可以照在圆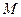 上,试求发出光线所在直线的斜率取值范围。
上,试求发出光线所在直线的斜率取值范围。
(本小题满分12分)如图在棱长为1正方体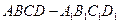 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系 ,
,
(I)若点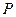 在线段
在线段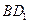 上,且满足
上,且满足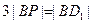 ,试写出点
,试写出点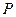 的坐标并写出
的坐标并写出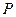 关于平面
关于平面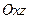 的对称点
的对称点 的坐标;
的坐标;
(Ⅱ)线段 中点为
中点为 ,求点
,求点 到点
到点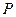 的距离。
的距离。
本小题满分12分)如图,给出了一个程序框图,其作用是输入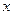 的值,输出相应的
的值,输出相应的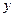 的值,
的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视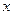 为自变量,
为自变量,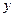 为函数值,试写出函数
为函数值,试写出函数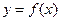 的解析式;
的解析式;
(Ⅲ)若要使输入的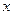 的值与输出的
的值与输出的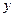 的值相等,则输入
的值相等,则输入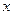 的值为多少?
的值为多少?

(本小题满分12分)已知两直线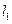 :
: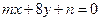 和
和 :
: ,
,
(I)若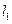 与
与 交于点
交于点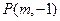 ,求
,求 的值;
的值;
(Ⅱ)若 ,试确定
,试确定 需要满足的条件。
需要满足的条件。