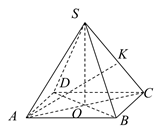
根据定积分的几何意义推出下列积分的值.
(1) 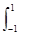 xdx; (2)
xdx; (2) cos xdx.
cos xdx.
设等差数列 的公差为
的公差为 ,且
,且 .若设
.若设 是从
是从 开始的前
开始的前 项数列的和,即
项数列的和,即 ,
, ,如此下去,其中数列
,如此下去,其中数列 是从第
是从第 开始到第
开始到第 )项为止的数列的和,即
)项为止的数列的和,即 .
.
(1)若数列 ,试找出一组满足条件的
,试找出一组满足条件的 ,使得:
,使得:  ;
;
(2)试证明对于数列 ,一定可通过适当的划分,使所得的数列
,一定可通过适当的划分,使所得的数列 中的各数都为平方数;
中的各数都为平方数;
(3)若等差数列 中
中 .试探索该数列中是否存在无穷整数数列
.试探索该数列中是否存在无穷整数数列 ,使得
,使得 为等比数列,如存在,就求出数列
为等比数列,如存在,就求出数列 ;如不存在,则说明理由.
;如不存在,则说明理由.
已知抛物线 .
.
(1)若圆心在抛物线 上的动圆,大小随位置而变化,但总是与直线
上的动圆,大小随位置而变化,但总是与直线 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;
(2)抛物线 的焦点为
的焦点为 ,若过
,若过 点的直线与抛物线相交于
点的直线与抛物线相交于 两点,若
两点,若 ,求直线
,求直线 的斜率;
的斜率;
(3)若过 正半轴上
正半轴上 点的直线与该抛物线交于
点的直线与该抛物线交于 两点,
两点, 为抛物线上异于
为抛物线上异于 的任意一点,记
的任意一点,记 连线的斜率为
连线的斜率为 试求满足
试求满足 成等差数列的充要条件.
成等差数列的充要条件.
某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布律和数学期望.
的分布律和数学期望.
对于函数 ,若在定义域存在实数
,若在定义域存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设 是定义在
是定义在 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
如图,设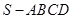 是一个高为
是一个高为 的四棱锥,底面
的四棱锥,底面 是边长为
是边长为 的正方形,顶点
的正方形,顶点 在底面上的射影是正方形
在底面上的射影是正方形 的中心.
的中心.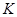 是棱
是棱 的中点.试求直线
的中点.试求直线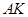 与平面
与平面 所成角的大小.
所成角的大小.