设等差数列
的公差为
，且
．若设
是从
开始的前
项数列的和，即
，
，如此下去，其中数列
是从第
开始到第
)项为止的数列的和，即
．
(1)若数列
,试找出一组满足条件的
,使得： 
；
(2)试证明对于数列
，一定可通过适当的划分，使所得的数列
中的各数都为平方数；
(3)若等差数列中
．试探索该数列中是否存在无穷整数数列
,使得为等比数列,如存在,就求出数列；如不存在，则说明理由．
（本小题满分14分）如图，在平面直角坐标系xOy中，椭圆C的中心在坐标原点O，右焦点为F．若C的右准线l的方程为x＝4，离心率e＝．
（1）求椭圆C的标准方程；
（2）设点P为直线l上一动点，且
在x轴上方．圆M经过O、F、P三点，求当圆心M到x轴的距离最小时圆M的方程．
（本小题满分14分）如图，在直三棱柱ABC－A1B1C1中，点D、E分别在边BC、
B1C1上，CD＝B1E＝AC，ÐA
CD＝60°．
求证：（1）BE∥平面AC1D；
（2）
平面ADC1⊥平面BCC1B1．
（本小题满
分14分）已知函数f(x)＝2
sinxco
sx－2sin2x．
（1）求函数f(x)的最小正周期；
（2）求函数f(x)在区间[－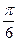
，
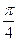]上的最大值和最小值．
已知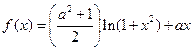
.
（1）
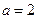时，求
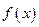的极值
（2）当
时，讨论
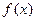的单调性。
（3）证明：
（
，
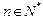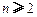，其中无理数
）
