某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容，成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示，其中“数学与逻辑”科目的成绩等级为B的考生有10人
（1）求该班考生中“阅读与表达”科目中成绩等级为A的人数；
（2）若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分，该考场共10人得分大于7分，其中2人10分，2人9分，6人8分，从这10人中随机抽取2人，求2人成绩之和
的分布列。
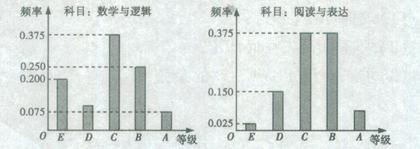
（本小题满分10分）选修4-4：坐标系与参数方程
在极坐标系中，已知圆
与直线
为参数）相切，求实数
的值。
（本小题满分10分）选修4—1；几何证明选讲
如图，在△ABC 中，
以AB为直径的⊙O交AC于D,点E为BC的中点，连接DE、AE, AE交⊙O于点F
(Ⅰ) 求证：
是⊙O的切线；
(Ⅱ) 若⊙O的直径为2，求
的值．
（本小题满分12分）已知
的图像在点
处的切线与直线
平行.
（1）求a，b满足的关系式；
（2）若
上恒成立，求a的取值范围；
（本小题满分12分）如图，在△ABC中，|AB|=|AC|=
，|BC|=2，以B、C为焦点的椭圆恰好过AC的中点P.
（Ⅰ）求椭圆的标准方程；
（Ⅱ） 过椭圆的右顶点作直线l与圆E：（x-1）2+y2=2相交于M、N两点，试探究点M、N能将圆E分割成弧长比值为1∶3的两段弧吗？若能，求出直线l的方程；若不能，请说明理由.
如图，在四棱锥P—ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，PA＝AB＝4， G为PD中点，E点在AB上，平面PEC⊥平面PDC.
（Ⅰ）求证：AG⊥平面PCD；
（Ⅱ）求证：AG∥平面PEC；
（Ⅲ）求点G到平面PEC的距离.