某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布律和数学期望.
的分布律和数学期望.
已知A,B,C三点的坐标分别为A(3,0),B(0,3),C(cosα,sinα),其中α∈(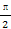 ,
, ).
).
(1)若| |=|
|=|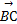 |,求角α的值.
|,求角α的值.
(2)若 ·
·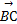 =-1,求tan(α+
=-1,求tan(α+ )的值.
)的值.
在平面直角坐标系中,已知向量a=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)(0≤θ≤ ).
).
(1)若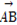 ⊥a,且|
⊥a,且|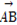 |=
|=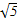 |
| |(O为坐标原点),求向量
|(O为坐标原点),求向量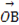 .
.
(2)若向量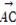 与向量a共线,当k>4,且tsinθ取最大值4时,求
与向量a共线,当k>4,且tsinθ取最大值4时,求 ·
·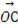 .
.
已知A(-1,0),B(0,2),C(-3,1), ·
·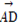 ="5,"
="5," 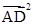 =10.
=10.
(1)求D点的坐标.
(2)若D点在第二象限,用 ,
,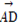 表示
表示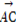 .
.
(3)设 =(m,2),若3
=(m,2),若3 +
+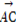 与
与 垂直,求
垂直,求 的坐标.
的坐标.
已知四点A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求实数x,使两向量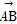 ,
, 共线.
共线.
(2)当两向量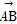 与
与 共线时,A,B,C,D四点是否在同一条直线上?
共线时,A,B,C,D四点是否在同一条直线上?
平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1),回答下列问题:
(1)求3a+b-2c.
(2)求满足a=mb+nc的实数m,n.
(3)若(a+kc)∥(2b-a),求实数k.