某大型企业人力资源部为了研究企业员工工作积极性和对企业改革态度的关系,随机抽取了189名员工进行调查,所得数据如下表所示:
| |
积极支持企业改革 |
不赞成企业改革 |
合计 |
| 工作积极 |
54 |
40 |
94 |
| 工作一般 |
32 |
63 |
95 |
| 合计 |
86 |
103 |
189 |
对于人力资源部的研究项目,根据上述数据能得出什么结论?
已知数列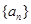 满足:
满足: ,
,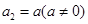 ,
, (其中
(其中 为非零常数,
为非零常数,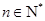 ).
).
(1)判断数列 是不是等比数列?
是不是等比数列?
(2)求 ;
;
(3)当 时,令
时,令 ,
, 为数列
为数列 的前
的前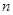 项和,求
项和,求 .
.
已知函数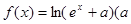 为常数,
为常数,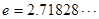 )是
)是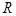 上的奇函数.
上的奇函数.
(Ⅰ)求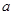 的值;(Ⅱ)讨论关于
的值;(Ⅱ)讨论关于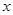 的方程
的方程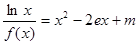 的根的个数.
的根的个数.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2 DE=2,M为AD中点.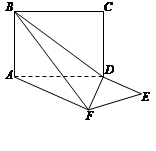
(Ⅰ) 证明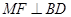 ;
;
(Ⅱ) 若二面角A-BF-D的平面角的余弦值为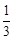 ,求AB的长.
,求AB的长.
某某种饮料每箱6听,如果其中有两听不合格产品.
(1)质检人员从中随机抽出1听,检测出不合格的概率多大?;
(2)质检人员从中随机抽出2听,设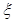 为检测出不合格产品的听数,求
为检测出不合格产品的听数,求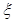 的分布列及数学期望.
的分布列及数学期望.
已知向量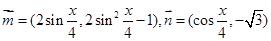 ,函数
,函数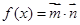 .
.
(1) 求函数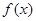 的最大值,并写出相应
的最大值,并写出相应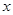 的取值集合;
的取值集合;
(2) 若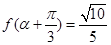 ,且
,且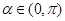 ,求
,求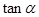 的值.
的值.