为了预防流感，某学校对教室采用药薰消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧后，y与x成反比例（如图），现测药物8分钟燃毕，此时空气中每立方米含药量为6毫克，请根据题中所提供的信息，回答下列问题：
（1）药物燃烧时，y关于x的函数关系式为 ，自变量x的取值范围是 ；药物燃烧完后，y与x的函数关系式为 ；
（2）研究表明，当空气中的每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过几分钟后，学生才能回到教室?
（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效地杀灭空气中的病菌，那么此次消毒是否有效？为什么？
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2,4），过点A作AB⊥y轴，垂足为B，连结OA。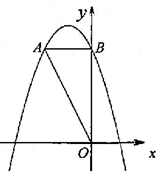
（1）求△OAB的面积；
（2）若抛物线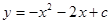
经过点A。
①求c的值；
②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围（直接写出答案即可）。
某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量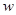
（千克）随销售单价
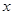（元/千克）的变化而变化，具体关系式为：
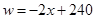，且物价部门规定这种绿茶的销售单价不得高于90元/千克．设这种绿茶在这段时间内的销售利润为
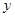（元），解答下列问题：
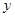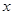（1）求与的关系式；
（2）当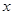取何值时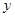，的值最大？
（3）如果公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？
如图，在直角坐标平面中，O为坐标原点，二次函数
的图象与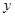
轴的负半轴相交于点C，点C的坐标为（0，-3），且BO＝CO。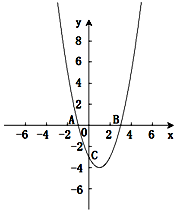
（1）求出B点坐标和这个二次函数的解析式
（2）求出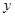随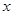
的增大而减小的自变量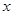的取值范围
用长度为32m的金属材料制成如图所示的金属框，下部为一个矩形，上部为一个等边三角形。当下部的矩形面积最大时，求矩形的AB、BC的边长各为多少m？并求此时整个金属框的面积是多少？
已知二次函数y=ax2＋bx－3的图象经过点A（2，－3），B（－1，0）．
（1）求二次函数的解析式；
（2）填空：要使该二次函数的图象与x轴只有一个交点，
应把图象沿y轴向上平移 __________个单位．