x为何值时,代数式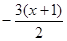 的值比代数式
的值比代数式 的值大.
的值大.
如图,已知AB∥CD,∠1=50°,BD平分∠ADC,求∠A的度数.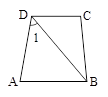
如图,直线 ,
, ,
, ,相交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
,相交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
如图,离河岸不远处有一个村庄,村民到岸边取水,怎样走最近?这什么?如果要到码头乘船,怎样走最近?为什么?
如图1,在平面直角坐标系中,点A、C分别在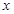 轴、
轴、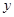 轴上,四边形OABC是面积为4的正方形,函数
轴上,四边形OABC是面积为4的正方形,函数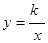 (
(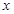 >0)的图象经过点B.
>0)的图象经过点B.
(1) =;
=;
(2)如图2,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′和正方形MA′BC.设线段MC′、NA′分别与函数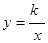 (
(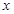 >0)的图象交于点E、F,则点E、F的坐标分别为:E (,),F (,);
>0)的图象交于点E、F,则点E、F的坐标分别为:E (,),F (,);
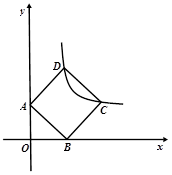
(3)如图3,面积为4的正方形ABCD的顶点A、B分别在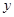 轴、
轴、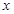 轴上,顶点C、D在反比例函数
轴上,顶点C、D在反比例函数 (
(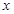 >0)的图像上,试求OA、OB的长。(请写出必要的解题过程)
>0)的图像上,试求OA、OB的长。(请写出必要的解题过程)

某次知识竞赛共有20道题,每一题答对得5分,答错或不答都扣3分.
(1)小明想要超过60分,那么小明至少要答对多少道题?
(2)小亮获得二等奖(70分~90分),请你算算小亮答对了几道题?