（本小题满分12分）
已知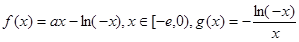
，其中
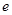是自然对数的底数，
（1）讨论
时，
的单调性。
（2）求证：在（1）条件下，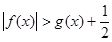
（3）是否存在实数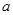
，使得最小值是3，如果存在，求出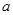的值；如果不存在，说明理由。
为了研究患慢性气管炎与吸烟量的关系，调查了228人，其中每天的吸烟支数在10支以上的20支以下的调查者中，患者人数有98人，非患者人数有89人，每天的吸烟支数在20支以上的调查者中，患者人数有25人，非患者人数有16人。
（1）根据以上数据建立一个2×2的列联表；
（2），试问患慢性气管炎是否与吸烟量相互独立？
参考公式：
 |
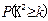0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
|
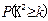0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
为调查吸烟是否对患肺癌有影响，某肿瘤研究所随机地调查了9965人，得到如下结果：（吸烟与患肺癌列联表）
| 不患肺癌 |
患肺癌 |
总计 |
|
| 不吸烟 |
7775 |
42 |
7817 |
| 吸烟 |
2099 |
49 |
2148 |
| 总计 |
9874 |
91 |
9965 |
那么吸烟是否对患肺癌有影响？
如何对草莓、橙子、桃子、苹果、梨等5种水果进行分类？
在研究某种新措施对猪白痢的防治效果问题时，得到了以下数据：
| 存活数 |
死亡数 |
合计 |
|
| 新措施 |
132 |
18 |
150 |
| 对照 |
114 |
36 |
150 |
| 合计 |
246 |
54 |
300 |
试利用图形和独立性检验来判断新措施对防治猪白痢是否有效？
研究人员选取170名青年男女大学生的样本，对他（她）们进行一种心理测验，发现有60名女生对该心理的最后一个题目的反应是：作肯定的18名，否定42名；男生110名在相同的项目上作出肯定的有22名，否定的有88名.请问性别与态度之间是否存在某种关系？请分别用图形与独立性检验的方法进行判断.