(本小题满分12分)已知
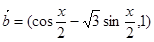
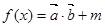
(1) 求 在
在 上的单调区间
上的单调区间
(2)当x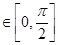 时,
时, 的最小值为2,求
的最小值为2,求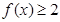 成立的
成立的 的取值集合。
的取值集合。
(3)若存在实数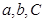 ,使得
,使得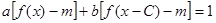 ,对任意x
,对任意x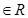 恒成立,
恒成立,
求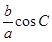 的值。
的值。
已知函数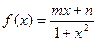 是定义在
是定义在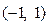 上的奇函数,且
上的奇函数,且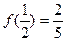
(1)求实数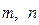 的值
的值
(2)用定义证明 在
在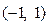 上是增函数
上是增函数
(3)解关于 的不等式
的不等式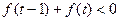
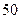
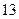
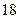

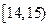
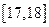
(Ⅰ)若成绩大于或等于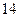 秒且小于
秒且小于 秒认为良好,求该班在这次百米测试中成绩良好的人数;
秒认为良好,求该班在这次百米测试中成绩良好的人数;
(Ⅱ)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于 的概率。
的概率。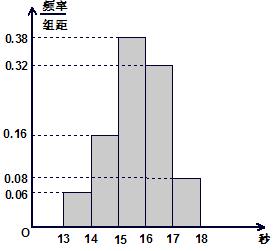
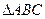
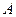
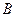

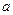
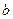
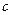
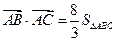
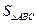
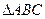
(Ⅰ)求 的值;
的值;
(Ⅱ)若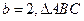 的面积
的面积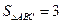 ,求
,求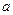 的值
的值

(Ⅰ)当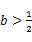 时,判断函数
时,判断函数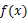 在定义域上的单调性。
在定义域上的单调性。
(Ⅱ)若函数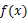 有极值点,求b的取值范围及
有极值点,求b的取值范围及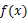 的极值点。
的极值点。
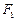


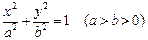
(Ⅰ)设椭圆 上的点
上的点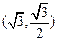 到两点
到两点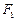 、
、 距离之和等于
距离之和等于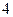 ,写出椭圆
,写出椭圆 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设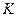 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点
的中点 的轨迹方程;
的轨迹方程;
(Ⅲ)设点 是椭圆
是椭圆 上的任意一点,过原点的直线
上的任意一点,过原点的直线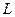 与椭圆相交于
与椭圆相交于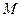 ,
,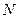 两点,当直线
两点,当直线 ,
,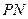 的斜率都存在,并记为
的斜率都存在,并记为 ,
, ,试探究
,试探究 的值是否与点
的值是否与点 及直线
及直线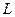 有关,不必证明你的结论。
有关,不必证明你的结论。