(本小题满分13分)矩形 中,
中, ,
, 是
是 中点,沿
中点,沿 将
将 折起到
折起到 的位置,使
的位置,使 ,
, 分别是
分别是 中点.
中点.
(1)求证: ⊥
⊥ ;
;
(2)设 ,求四棱锥
,求四棱锥 的体积.
的体积.
(本小题满分13分)
某种有奖销售的饮料,瓶 盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为
盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 甲、乙、丙三位同学每人购买一瓶该饮料。
甲、乙、丙三位同学每人购买一瓶该饮料。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数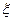 的分布列及数学期望
的分布列及数学期望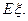
(本小题满分13分)
已知向量 且与向量
且与向量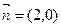 所成角为
所成角为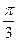 ,其中A,B,C是
,其中A,B,C是 的内角。
的内角。
(1)求角B的大小;
(2)求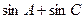 的取值范围。
的取值范围。
(本小题满分1 3分)
3分)
已知等差数 列
列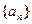 满足
满足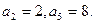
(1)求数列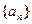 的通项公式;
的通项公式;
(2)设各项均为正数的等比数列 的前n项和为Tn若
的前n项和为Tn若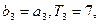 求Tn。
求Tn。
(本小题满分5分)选修4—5:不等式选讲
已知函数
(1)作出函数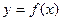 的图象;
的图象;
(2)解不等式
(本小题满分5分)选修4—4:坐标系与参数方程
已知直线 与圆
与圆 (
( 为参数),试判断它们的公共点个数。
为参数),试判断它们的公共点个数。