(本小题满分14分)关于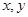 的方程
的方程
(1)若方程C表示圆,求实数m的取值范围;
(2)在方程C表示圆时,若该圆与直线
且 ,求实数m的值;
,求实数m的值;
(3)在(2)的条件下,若定点A的坐标为(1,0),点P是线段MN上的动点,
求直线AP的斜率的取值范围。
已知双曲线 的焦点与椭圆
的焦点与椭圆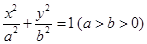 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为 ,
, 是椭圆上的的动点.
是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: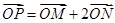 ,直线
,直线 与
与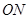 的斜率之积为
的斜率之积为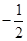 ,求证:存在定点
,求证:存在定点 ,
,
使得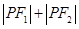 为定值,并求出
为定值,并求出 的坐标;
的坐标;
(3)若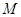 在第一象限,且点
在第一象限,且点 关于原点对称,点
关于原点对称,点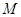 在
在 轴的射影为
轴的射影为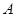 ,连接
,连接 并延长交椭圆于
并延长交椭圆于
点 ,求证:以
,求证:以 为直径的圆经过点
为直径的圆经过点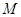 .
.
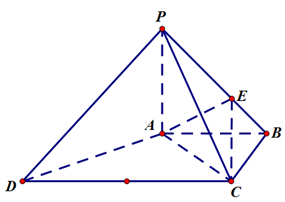
如图,四棱锥 中,
中,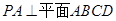 ,底面
,底面 为梯形,
为梯形,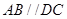 ,
, ,且
,且 ,
, .
.
(1)求证: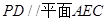 ;
;
(2)求二面角 的余弦值.
的余弦值.
设 表示数列
表示数列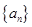 的前
的前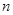 项和.
项和.
(1)若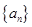 为公比为
为公比为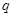 的等比数列,写出并推导
的等比数列,写出并推导 的计算公式;
的计算公式;
(2)若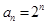 ,
, ,求证:
,求证: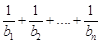 <1.
<1.
某校高一年级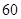 名学生参加数学竞赛,成绩全部在
名学生参加数学竞赛,成绩全部在 分至
分至 分之间,现将成绩分成以下
分之间,现将成绩分成以下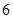 段:
段:
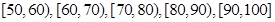 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 
(1)求成绩在区间 的频率;
的频率;
(2)从成绩大于等于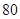 分的学生中随机选
分的学生中随机选 名学生,其中成绩在
名学生,其中成绩在 内的学生人数为
内的学生人数为 ,求
,求 的分布列与均值.
的分布列与均值.
设锐角三角形ABC的内角A,B,C的对边分别为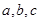 ,且
,且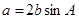 .
.
(1)求角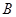 的大小;
的大小;
(2)若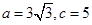 ,求
,求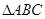 的面积及
的面积及 .
.