(本小题满分14分)已知函数 ,
,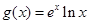 .(其中
.(其中 为自然对数的底数),
为自然对数的底数),
(Ⅰ)设曲线 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求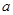 的值;
的值;
(Ⅱ)若对于任意实数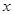 ≥0,
≥0,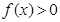 恒成立,试确定实数
恒成立,试确定实数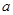 的取值范围;
的取值范围;
(Ⅲ)当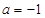 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点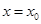
处的切线与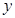 轴垂直?若存在,求出
轴垂直?若存在,求出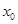 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数
,
.
(I)证明:当
时,
在
上是增函数;
(II)对于给定的闭区间
,试说明存在实数
,当
时,
在闭区间
上是减函数;
(III)证明:
.
已知数列
, 与函数
,
,
满足条件:
,
.(
)
与函数
,
,
满足条件:
,
.(
)
(I)若
,
,
存在,求
的取值范围;
(II)若函数
为
上的增函数,
,
,
,证明对任意
,
(用
表示).
已知正三角形
的三个顶点都在抛物线
上,其中
为坐标原点,设圆
是
的内接圆(点
为圆心)
(I)求圆
的方程;
(II)设圆
的方程为
,过圆
上任意一点
分别作圆
的两条切线
,切点为
,求
的最大值和最小值.
某企业准备投产一批特殊型号的产品,已知该种产品的成本
与产量
的函数关系式为
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格
与产量
的函数关系式如下表所示:

设
分别表示市场情形好、中差时的利润,随机变量
,表示当产量为
,而市场前景无法确定的利润.
(I)分别求利润
与产量
的函数关系式;
(II)当产量
确定时,求期望
;
(III)试问产量
取何值时,
取得最大值.
如图,在直三棱柱
中,
,
,
分别为棱
的中点,
为棱
上的点,二面角
为
.
(I)证明:
;
(II)求
的长,并求点
到平面
的距离.
