如图，2012年春节，摄影爱好者S在某公园A处，发现正前方B处有一立柱，测得立柱顶端O的仰角和立柱底部B的俯角均为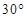
，已知S的身高约为
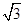米（将眼睛距地面的距离按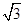米处理）
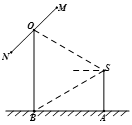
(1) 求摄影者到立柱的水平距离和立柱的高度；
(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转．摄影者有一视角范围为
的镜头，在彩杆转动的任意时刻，摄影者是否都可以将彩杆全部摄入画面？说明理由．
已知抛物线y2=2px(p>0)过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,|AB|≤2p.
(1)求实数a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
过抛物线y2=4x的准线与对称轴的交点作直线,交抛物线于M、N两点,问直线的倾斜角多大时,以线段MN为直径的圆经过抛物线的焦点?
某电厂冷却塔外形是如图1-7-8所示的双曲线的一部分绕其中轴(双曲线的虚轴)旋转所成的曲面,其中A,A′是双曲线的顶点,C,C′是冷却塔上口直径的两个端点,B,B′是冷却塔下底直径的两个端点,已知AA′="14" m,CC′="18" m,BB′="22" m,塔高20 m.
图1-7-8
(1)建立坐标系并写出该曲线的方程;
(2)求冷却塔的容积(精确到10 m3,塔壁厚度不计,π取3.14).
作用于某一质点的力F(x)=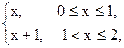
求力所做的功.
设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积.