已知函数f(x)=lnx+
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2 l+ 1n22,+…+ln2 n> ∈N*).
∈N*).
已知函数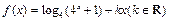 是偶函数。
是偶函数。
(1)求 的值;
的值;
(2)若方程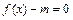 有解,求
有解,求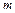 的取值范围。
的取值范围。
(10分)已知集合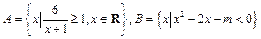 。
。
(1)当 时,求
时,求 ;
;
(2)当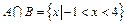 ,求实数
,求实数 的值。
的值。
已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上。(1)求a1和a2的值;(2)求数列{an},{bn}的通项an和bn;
14分)如图,半圆O的半径为2,A为直径延长线上的一点,且OA=4,B为半圆周上任意一点,从AB向外作等边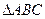 ,设
,设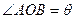 ,(1)将AB的长用
,(1)将AB的长用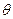 表示,(2)将四边形OACB的面积用
表示,(2)将四边形OACB的面积用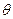 表示,(3)问当
表示,(3)问当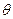 为何值时,四边形OACB的面积最大?最大面积是多少?
为何值时,四边形OACB的面积最大?最大面积是多少?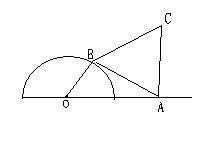
(14分) 制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙两个项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?