(本小题满分12分)某项计算机考试按科目A、科目B依次进行,只有大拿感科目A成绩合格时,才可继续参加科目B的考试,已知每个科目只允许有一次补考机会,两个科目均合格方快获得证书,现某人参加这项考试,科目A每次考试成绩合格的概率为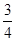 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为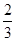 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这次考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为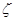 ,求随即变量
,求随即变量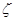 的分布列和数学期望.
的分布列和数学期望.
已知两定点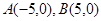 ,
,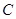 为动点
为动点
(1)若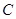 在x轴上方,且
在x轴上方,且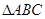 是等腰直角三角形,求
是等腰直角三角形,求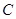 点坐标;
点坐标;
(2)若直线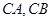 的斜率乘积为
的斜率乘积为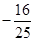 ,求
,求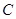 点坐标
点坐标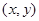 满足的关系式。
满足的关系式。
已知直线l:3x-y+3=0,求:
(1)过点P(4,5)且与直线l垂直的直线方程;
(2)与直线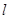 平行且距离等于
平行且距离等于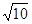 的直线方程。
的直线方程。
已知无穷数列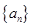 的前
的前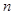 项和为
项和为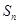 ,且满足
,且满足 ,其中
,其中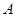 、
、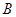 、
、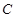 是常数.
是常数.
(1)若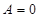 ,
,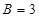 ,
,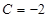 ,求数列
,求数列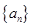 的通项公式;
的通项公式;
(2)若 ,
,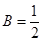 ,
, ,且
,且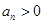 ,求数列
,求数列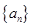 的前
的前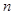 项和
项和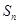 ;
;
(3)试探究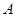 、
、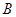 、
、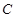 满足什么条件时,数列
满足什么条件时,数列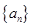 是公比不为
是公比不为 的等比数列.
的等比数列.
已知函数 .
.
(1)若 ,当
,当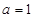 时,求
时,求 的取值范围;
的取值范围;
(2)若定义在 上奇函数
上奇函数 满足
满足 ,且当
,且当 时,
时, ,求
,求 在
在 上的反函数
上的反函数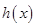 ;
;
(3)若关于 的不等式
的不等式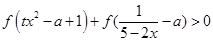 在区间
在区间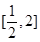 上有解,求实数
上有解,求实数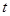 的取值范围.
的取值范围.
钓鱼岛及其附属岛屿是中国固有领土,如图:点A、B、C分别表示钓鱼岛、南小岛、黄尾屿,点C在点A的北偏东47°方向,点B在点C的南偏西36°方向,点B在点A的南偏东79°方向,且A、B两点的距离约为3海里.
(1)求A、C两点间的距离;(精确到0.01)
(2)某一时刻,我国一渔船在A点处因故障抛锚发出求救信号.一艘R国舰艇正从点C正东10海里的点P处以18海里/小时的速度接近渔船,其航线为P C
C A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.
A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.