(本小题满分13分)
已知函数
(1)判断 的单调性;
的单调性;
(2)记 若函数
若函数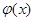 有两个零点
有两个零点 ,求证
,求证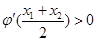
在直角坐标系XOY中,圆C: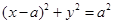 ,圆心为C,圆C与直线
,圆心为C,圆C与直线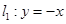 的一个交点的横坐标为2.
的一个交点的横坐标为2.
(1)求圆C的标准方程;
(2)直线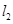 与
与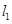 垂直,且与圆C交于不同两点A、B,若
垂直,且与圆C交于不同两点A、B,若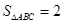 ,求直线
,求直线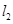 的方程.
的方程.
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,△PAD是正三角形,四边形ABCD是矩形,且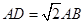 ,E为PB的中点.
,E为PB的中点.
(1)求证:PD∥平面ACE;
(2)求证:AC⊥PB
已知各项均为正数的等差数列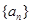 的公差为d,其前n项和为
的公差为d,其前n项和为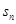 ,
, 且
且 成等比数列.
成等比数列.
(1)求公差d和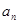 ;
;
(2)令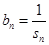 , 求数列
, 求数列 的前n项和
的前n项和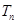 .
.
一袋中装有5个球,编号分别为1,2,3,4,5;设编号为n的球重量为 ; 这些球等可能地从袋中取出。
; 这些球等可能地从袋中取出。
(1)任取1球,试求其重量大于编号的概率;
(2)不放回先后逐一取出2球,求他们质量相等的概率。
已知函数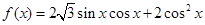
(1)求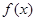 的最小正周期;
的最小正周期;
(2)当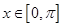 时,求
时,求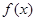 的单调递增区间。
的单调递增区间。