如图,圆柱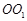 内有一个三棱柱
内有一个三棱柱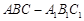 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.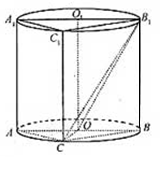
(Ⅰ)证明:平面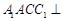 平面
平面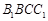 ;
;
(Ⅱ)设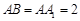 ,在圆柱
,在圆柱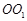 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱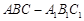 内的概率为
内的概率为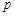 .
.
(ⅰ)当点C在圆周上运动时,求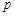 的最大值;
的最大值;
(ii)记平面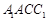 与平面
与平面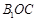 所成的角为
所成的角为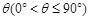 ,当
,当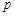 取最大值时,求
取最大值时,求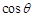 的值.
的值.
(本小题满分12分)椭圆G 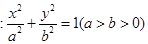 的长轴为4
的长轴为4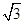 ,焦距为4
,焦距为4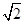 .
.
(1)求椭圆G的方程;
(2)若斜率为1的直线l与椭圆G交于A、B两点, 且点P(-3,2)在线段AB的垂直平分线上,求PAB的面积.
(本小题满分12分)等差数列{an}满足:a1=1, a2+a6=14;正项等比数列{bn}满足:b1=2,b3 =8.
(1)求数列{an},{bn}的通项公式an,bn;
(2)求数列{an·bn}的前n项和Tn.
(本小题满分12分)交通指数是指交通拥堵指数或交通运行指数(Traffic Performance Index,即“TPI”),是反应道路畅通或拥堵的概念性数值,交通指数的取值范围为0~10,分为五级:0~2畅通,2~4为基本畅通,4~6轻度畅通,6~8为中度拥堵,8~10为严重拥堵.高峰时段,巴中市交通指挥中心随机选取了市区40个交通路段,依据交通指数数据绘制的频率分布直方图如图所示:
(1)求出图中x的值,并计算这40个路段中为“中度拥堵”的有多少个?
(2)在我市区的40个交通路段中用分层抽样的方法抽取容量为20的样本.从这个样本路段的“基本畅通”和“严重拥堵”路段中随机选出2个路段,求其中只有一个是“严重拥堵”路段的概率.
(本小题满分12分)如图,直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱C1的中点,且CF⊥AB,AC=BC.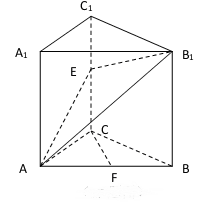
(1)求证:CF∥平面AEB1;
(2)求证:平面AEB1⊥平面ABB1A1.
(本小题满分10)已知函数f(x)=  sinx·cosx+
sinx·cosx+ cos2x+a-2 .
cos2x+a-2 .
(1)求函数f(x)的单调递增区间;
(2)设函数f(x)在[0,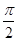 ]上的最小值为-
]上的最小值为- ,求函数f(x)(x∈R)的值域.
,求函数f(x)(x∈R)的值域.