(本小题满分12分)如图,直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱C1的中点,且CF⊥AB,AC=BC.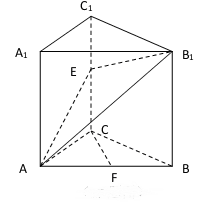
(1)求证:CF∥平面AEB1;
(2)求证:平面AEB1⊥平面ABB1A1.
已知函数 将
将 的图象向右平移2个单位,得到
的图象向右平移2个单位,得到 的图象.
的图象.
(1)求函数 的解析式;
的解析式;
(2) 若函数 与函数
与函数 的图象关于直线
的图象关于直线 对称,求函数
对称,求函数 的解析式;
的解析式;
(3)设 已知
已知 的最小值是
的最小值是 ,且
,且 求实数
求实数 的
的 取值范围.
取值范围.
(本题满分14分
某工厂生产一种产品的成本费由三部分组成
①职工工资固定支出 元
元
②原材料费每件40元
③电力与机器保养等费用为每件 元,其中
元,其中 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费 (元)表示成产品件数
(元)表示成产品件数 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量 不超过
不超过 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价 与产品件数
与产品件数 有如下关系:
有如下关系: ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
.
设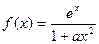 ,其中
,其中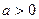
(Ⅰ)当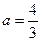 时,求
时,求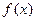 的极值点;
的极值点;
(Ⅱ)若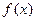 为R上的单调函数,求a的取值范围。
为R上的单调函数,求a的取值范围。
已知向量m=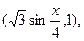 n=
n=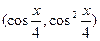
(1)若m·n=1,求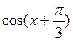 的值
的值
(2)记函数f(x)= m·n,在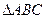 中,角A,B,C的对边分别是a,b,c,且满足
中,角A,B,C的对边分别是a,b,c,且满足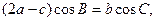 求f(A)的取值范围.
求f(A)的取值范围.
已知命题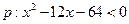 ,
,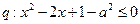 ,
,
若 是
是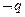 的必要而不充分条件,求正实数
的必要而不充分条件,求正实数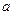 的取值范围
的取值范围