(本小题满分10分)设命题p:函数 的定义域为R, 命题q:双曲线
的定义域为R, 命题q:双曲线 的离心率
的离心率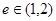 ,
,
(1)如果p是真命题,求实数 的取值范围;
的取值范围;
(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数 的取值范围.
的取值范围.
在△ 中,角
中,角 所对的边分别为
所对的边分别为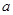 、
、 、
、 .若
.若 =
=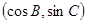 ,
, =
=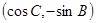 ,且
,且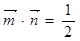 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若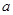 =
=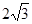 ,三角形面积
,三角形面积 =
=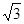 ,求
,求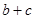 的值.
的值.
已知函数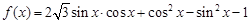 (
( )
)
(Ⅰ)求函数 的周期和递增区间;
的周期和递增区间;
(Ⅱ)若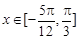 ,求
,求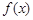 的取值范围.
的取值范围.
不等式选讲.
设函数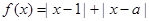 .
.
(1)若 解不等式
解不等式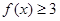 ;
;
(2)如果关于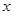 的不等式
的不等式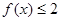 有解,求
有解,求 的取值范围.
的取值范围.
坐标系与参数方程.
在直角坐标系xoy中,直线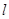 的参数方程为
的参数方程为 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为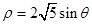 .
.
(1)求圆C的直角坐标方程;
(2)设圆C与直线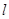 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为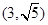 ,求|PA|+|PB|.
,求|PA|+|PB|.
几何证明选讲.
如图,直线 过圆心
过圆心 ,交⊙
,交⊙ 于
于 ,直线
,直线 交⊙
交⊙ 于
于 (不与
(不与 重合),直线
重合),直线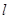 与⊙
与⊙ 相切于
相切于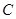 ,交
,交 于
于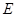 ,且与
,且与 垂直,垂足为
垂直,垂足为 ,连结
,连结 .
.
求证:(1)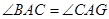 ;
;
(2)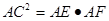 .
.