在 中,角
中,角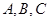 所对的边分别为
所对的边分别为 ,且
,且 .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若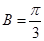 ,
,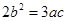 ,求
,求 的值
的值
口袋里装有7个大小相同小球, 其中三个标有数字1, 两个标有数字2, 一个标有数字3, 一个标有数字4.
(Ⅰ) 第一次从口袋里任意取一球, 放回口袋里后第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为 . 当
. 当 为何值时, 其发生的概率最大? 说明理由;
为何值时, 其发生的概率最大? 说明理由;
(Ⅱ) 第一次从口袋里任意取一球, 不再放回口袋里, 第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为 . 求
. 求 的分布列和数学期望.
的分布列和数学期望.
已知函数
 ).
).
(Ⅰ) 若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ) 若函数 在其图象上任意一点
在其图象上任意一点 处切线的斜率都小于
处切线的斜率都小于 ,求实数
,求实数 的取值范围.
的取值范围.
已知 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;(2)求展开式中的常数项;
从5名男同学与4名女同学中选3名男同学与2名女同学,分别担
任语文、数学、英语、物理、化学科代表.
(1)共有多少种不同的选派方法?
(2)若女生甲必须担任语文科代表,共有多少种不同的选派方法?
(3)若男生乙不能担任英语科代表,共有多少种不同的选派方法?
(本小题满分14分)已知:以点C (t,  )(t∈R , t≠ 0)为圆心的圆与
)(t∈R , t≠ 0)为圆心的圆与 轴交于点O, A,
轴交于点O, A,
与y轴交于点O, B,其中O为原点.
(Ⅰ)当t=2时,求圆C的方程;
(Ⅱ)求证:△OAB的面积为定值;
(Ⅲ)设直线y = –2x+4与圆C交于点M, N,若 ,求圆C的方程.
,求圆C的方程.