(本小题满分14分)已知:以点C (t,  )(t∈R , t≠ 0)为圆心的圆与
)(t∈R , t≠ 0)为圆心的圆与 轴交于点O, A,
轴交于点O, A,
与y轴交于点O, B,其中O为原点.
(Ⅰ)当t=2时,求圆C的方程;
(Ⅱ)求证:△OAB的面积为定值;
(Ⅲ)设直线y = –2x+4与圆C交于点M, N,若 ,求圆C的方程.
,求圆C的方程.
如图:是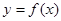 =
=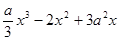 的导函数
的导函数
 的简图,它与
的简图,它与 轴的交点是(1,0)和(3,0)
轴的交点是(1,0)和(3,0)
(1)求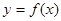 的极小值点和单调减区间;
的极小值点和单调减区间;
(2)求实数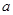 的值.
的值.
已知关于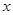 的不等式
的不等式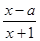 <0的解集为
<0的解集为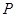 ,
,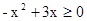 的解集为Q。
的解集为Q。
(Ⅰ)若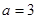 ,求集合
,求集合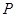 ;
;
(Ⅱ)若 ,求正数
,求正数 的取值范围。
的取值范围。
设函数 ,其中
,其中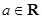 .
.
(1)若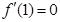 ,求a的值;
,求a的值;
(2)当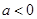 时,讨论函数
时,讨论函数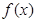 在其定义域上的单调性.
在其定义域上的单调性.
某市旅游部门开发一种旅游纪念品,每件产品的成本是 元,销售价是
元,销售价是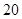 元,月平均销售
元,月平均销售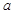 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为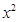 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是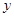 (元).
(元).
(1)写出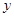 与
与 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
在数列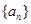 中,
中, ,
, ,
, 。
。
(Ⅰ)计算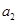 ,
,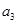 ,
, 的值;
的值;
(Ⅱ)猜想数列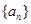 的通项公式,并用数学归纳法加以证明
的通项公式,并用数学归纳法加以证明