(本题12分)
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。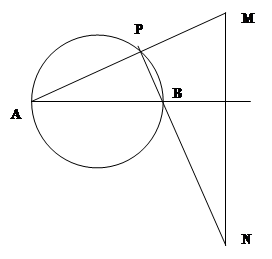
(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
一次函数 与指数型函数
与指数型函数 ,(
,(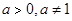 )的图像交于两点
)的图像交于两点 ,解答下列各题
,解答下列各题 :
:
(1)求一次函数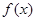 和指数型函数
和指数型函数 的表达式;
的表达式;
(2)作出这两个函数的图像;
(3)填空:当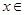 时,
时,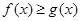 ;当
;当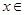 时,
时,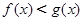 。
。
已知函数 的最小正周期为
的最小正周期为 ,最小值为
,最小值为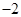 ,图象过点
,图象过点 ,(1)求
,(1)求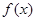 的解析式;(2)求满足
的解析式;(2)求满足 且
且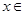
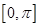 的
的 的集合.
的集合.
已知函数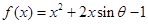 ,
,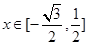
(1)当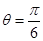 时,求
时,求 的最大值和最小值
的最大值和最小值
(2)若 在
在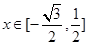 上是单调函数,且
上是单调函数,且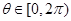 ,求
,求 的取值范围
的取值范围
已知 为第三象限角,
为第三象限角, .
.
(1)化简
(2)若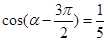 ,求
,求 的值
的值
(本小题满分14分)
已知动圆P(圆心为点P)过定点A(1,0),且与直线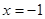 相切。记动点P的轨迹为C。
相切。记动点P的轨迹为C。
(Ⅰ)求轨迹C的方程;
(Ⅱ)设过点P的直线l与曲线C相切,且与直线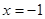 相交于点Q。试研究:在x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。
相交于点Q。试研究:在x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。