(本小题满分12分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
6 |
0.08 |
| 60.5~70.5 |
|
0.16 |
| 70.5~80.5 |
15 |
|
| 80.5~90.5 |
24 |
0.32 |
| 90.5~100.5 |
|
|
| 合计 |
75 |
|
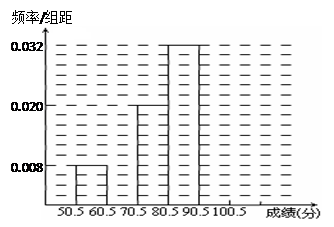
(Ⅰ)填充频率分布表的空格(将答案直接填在答题卡的表格内);
(Ⅱ)补全频率分布直方图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
(Ⅰ)求正三棱柱的侧棱长.
(Ⅱ)若M为BC1的中点,试用基底向量 、
、 、
、 表示向量
表示向量 ;
;
(Ⅲ)求异面直线AB1与BC所成角的余弦值.
已知 ;¬
;¬ 是¬
是¬ 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列 的前4项,后6组的频数从左到右依次是等差数列
的前4项,后6组的频数从左到右依次是等差数列 的前6项.
的前6项.
(Ⅰ)求等比数列 的通项公式;
的通项公式;
(Ⅱ)求等差数列 的通项公式;
的通项公式;
(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率 的大小.
的大小.
已知等腰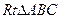 中,
中, .
.
(Ⅰ)在线段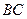 上任取一点
上任取一点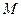 ,求使
,求使 的概率;
的概率;
(Ⅱ)在 内任作射线
内任作射线 ,求使
,求使 的概率.
的概率.
(本题满分18分,第1小题满分6分,第2小题满分6分,第3小题满分6分)
已知函数 ,如果存在给定的实数对(
,如果存在给定的实数对( ),使得
),使得 恒成立,则称
恒成立,则称 为“S-函数”.
为“S-函数”.
(1)判断函数 是否是“S-函数”;
是否是“S-函数”;
(2)若 是一个“S-函数”,求出所有满足条件的有序实数对
是一个“S-函数”,求出所有满足条件的有序实数对 ;
;
(3)若定义域为 的函数
的函数 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对 和
和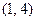 ,当
,当 时,
时, 的值域为
的值域为 ,求当
,求当 时函数
时函数 的值域.
的值域.