某海域有
、
两个岛屿，岛在岛正东4海里处。经多年观察研究发现，某种鱼群洄游的路线是曲线
，曾有渔船在距岛、岛距离和为8海里处发现过鱼群。以、所在直线为
轴，
的垂直平分线为
轴建立平面直角坐标系。
（1）求曲线的标准方程；
（2）某日，研究人员在、两岛同时用声纳探测仪发出不同频率的探测信号（传播速度相同），、两岛收到鱼群在
处反射信号的时间比为
，问你能否确定处的位置（即点的坐标）？
（本小题满分13分）已知函数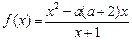
（
）.
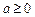（I）当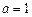
时，求
在点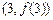
处的切线方程；
（Ⅱ）求函数在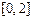
上的最小值.
（本小题满分12分）某新型智能在线电池的电量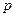
（单位：kwh）随时间
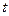（单位：小时）的变化规律是：
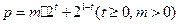，其中
是智能芯片实时控制的参数。
（1）当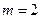
时，求经过多少时间电池电量是
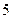kwh；
（2）如果电池的电量始终不低于2 kwh，求参数的取值范围
（本小题满分13分）
设函数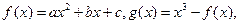
（
）若
上是增函数，在（0，1）上是减函数，函数
在R上有三个零点，且1是其中一个零点。
（1）求b的值；
（2）求
最小值的取值范围。
（本小题满分12分）
已知命题
：方程
在
上有且仅有一解；命题
：只有一个实数
满足不等式
若命题
是假命题，求实数
的取值范围.
（本小题满分12分）函数
的定义域为集合A，关于x的不等式
的解集为B，求使
的实数
的取值范围。